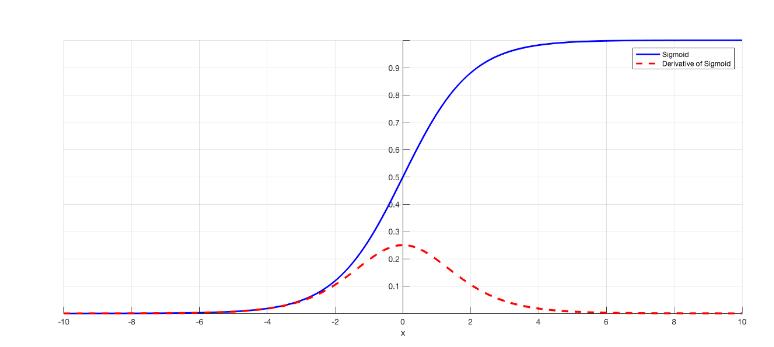
Dans cet article, nous verrons la dérivation complète de la fonction sigmoïde telle qu’utilisée dans les applications d’intelligence artificielle.

$$ \bbox[white,8px,border:1px solid black] { \sigma (x) = \frac{1}{1+e^{-x}} } $$

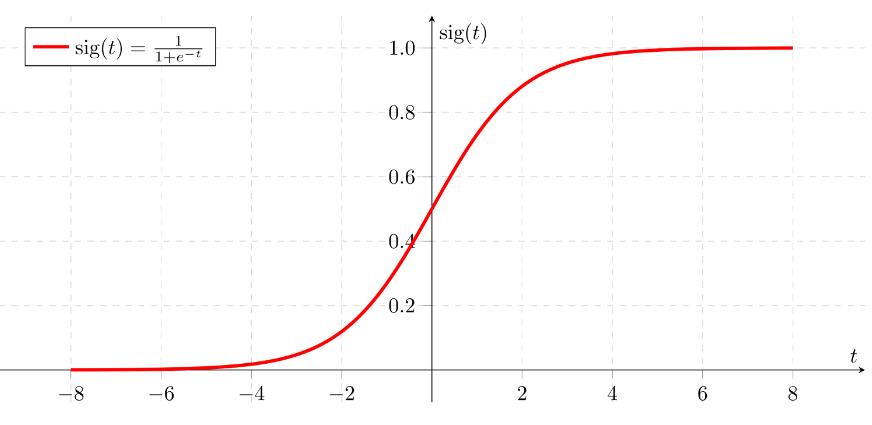
Lorsque la valeur de n devient plus grande, la valeur de la fonction sigmoïde devient de plus en plus proche de 1 et lorsque n devient plus petit, la valeur de la fonction sigmoïde devient de plus en plus proche de 0.

$$ \bbox[white,8px,border:1px solid black] { \frac{d \sigma (x)}{dt} = -(1 – e^{-x})^{-2} \frac{d}{dx} (1+e^{-x}) = -(1 – e^{-x})^{-2} e^{-x} = \frac{1}{1+e^{-x}} (1- \frac{1}{1+e^{-x}}) = \sigma (x) (1- \sigma (x)) } $$