| Un produit scalaire (dot product) d’un vecteur ${\bf v} = (v_1,v_2)$ et ${\bf w} =(w_1,w_2)$ est le nombre ${\bf v.w}$ tel que $$ \bbox[white,8px,border:1px solid black] { \begin{equation} {\bf v.w} = v_1 w_1 + v_2 w_2 \end{equation} } $$ |
| La longueur $||{\bf x}||$ d’un vecteur ou norme ${\bf v}$ est la racine carrée de ${\bf v.v}$
$$ \bbox[white,8px,border:1px solid black] |
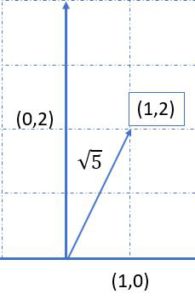
$ norme = ||x|| = {\bf \sqrt{v.v}} = (v_1^2 + v_2^2 )^{1/2} = 1^2 + 2^2 = 5 $
Si ${\bf v} = (1,3,2)$, ${\bf v.v}=1+9+4=14$ et sa longueur sera égale à $\sqrt 14$.
| Un vecteur unitaire est un vecteur dont la norme est égale à 1. Ainsi ${\bf v.v = 1} $ |
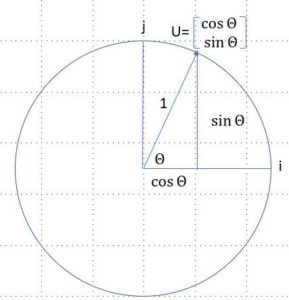Voici des exemples de vecteurs unitaires $i = \dbinom 1 0$, $j = \dbinom 0 1$ et $u= \dbinom {\sin \theta} {\cos \theta} $ car ${\sin \theta} ^2 + {\cos \theta}^2=1$.
Quand $\theta$ est nul, le vecteur horizontal est i. Quand $\theta$ est égal à 90°, le vecteur vertical est j.
Les deux vecteurs ${\bf v}=(4,2)$ et ${\bf w}=(-1,2)$ ont un produit scalaire égal à 0 et sont perpendiculaires.
Norme
Soit V un espace vectoriel sur K (K étant un corps commutatif $\mathbb{R}$ ou $\mathbb{C}$)
Une fonction ||·|| : V → R est une norme de vecteur si pour tout \(x,y \in V\) $\rto$
$a+1 \above 1pt b$
|\(x\)|
$$
\begin{matrix}(
a & b \\
c & d
\end{matrix}
\quad
\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}
\quad
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
\quad
\begin{vmatrix}
a & b \\
c & d
\end{vmatrix}
\quad
\begin{Vmatrix}
a & b \\
c & d
\end{Vmatrix}
$$
\[\frac{a}{b} ou \dfrac{a}{b}\]
\[\mathbb{A B C D E F G H I J K L M}\]
\begin{verbatim}
\[\mathbb{A B C D E F G H I J K L M}\]
\end{verbatim}
$$\forall \mathbf{x}\in\mathcal{A}
\textrm{ we have } \mathbf{x}^2 =1$$
\begin{verbatim}
$$\forall \mathbf{x}\in\mathcal{A}
\textrm{ we have } \mathbf{x}^2 =1$$
\end{verbatim}