Envisageons de représenter un document par un vecteur dont chaque composante correspond au nombre d’occurrences d’un mot particulier dans un document. La langue anglaise a de l’ordre de 25 000 mots. Ainsi, un tel document est représenté par un vecteur de 25 000 dimensions. La représentation d’un document s’appelle le modèle de vecteur de mot.
Une collection de n documents peut être représentée par une collection de vecteurs 25 000-imensionnels, un vecteur par document. Les vecteurs peuvent être disposés en colonnes d’une matrice de 25 000 × n.
Un autre exemple de données de haute dimension se pose dans les données client-produit. S’il y a 1 000 produits à vendre et un grand nombre de clients, l’enregistrement du nombre de fois que chaque client achète chaque produit donne lieu à une collection de vecteurs de dimension 1000.
Il existe de nombreux autres exemples où chaque enregistrement d’un ensemble de données est représenté par un vecteur de grande dimension. Considérez une collection de n pages Web liées. Un lien est un pointeur d’une page Web à une autre. Chaque page web peut être représentée par un vecteur 0-1 avec n composantes où la j ème composante du vecteur représentant la page web i ème a la valeur 1, si et seulement s’il y a un lien de la i ème page web vers la j ème page web.
Dans la représentation de l’espace vectoriel des données, les propriétés des vecteurs tels que les produits scalaires, la distance entre les vecteurs et l’orthogonalité ont souvent des interprétations naturelles.
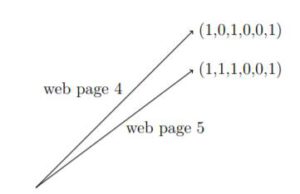 Par exemple, la distance au carré entre deux vecteurs 0-1 représentant des liens sur des pages Web est le nombre de pages Web auxquelles une seule d’entre elles est lié.. Ainsi, ci-contre, les pages 4 et 5 ont toutes deux des liens vers les pages 1, 3 et 6, mais seule la page 5 a un lien vers la page 2. Ainsi, la distance au carré entre les deux vecteurs est égale à un.
Par exemple, la distance au carré entre deux vecteurs 0-1 représentant des liens sur des pages Web est le nombre de pages Web auxquelles une seule d’entre elles est lié.. Ainsi, ci-contre, les pages 4 et 5 ont toutes deux des liens vers les pages 1, 3 et 6, mais seule la page 5 a un lien vers la page 2. Ainsi, la distance au carré entre les deux vecteurs est égale à un.
Lorsqu’une nouvelle page Web est créée, une question naturelle est de savoir quelles sont les pages les plus proches, c’est-à-dire les pages qui contiennent un ensemble similaire de liens. Cette question se traduit par celle géométrique qui consiste à trouver les voisins les plus proches. La requête du voisin le plus proche doit recevoir une réponse rapide : plus loin, nous verrons un théorème de type géométrique, appelé le théorème de projection aléatoire : si chaque page web est un vecteur d-imensionnel, alors au lieu de passer le temps d à lire le vecteur dans son intégralité, une fois la projection aléatoire dans un espace de dimension k, il suffit de lire k entrées par vecteur.
 Les produits scalaires jouent également un rôle utile. Dans l’exemple ci-contre, deux documents contenant plusieurs des mêmes mots sont considérés comme similaires. Une façon de mesurer la co-occurrence de mots dans deux documents est de prendre le produit scalaire des vecteurs représentant les deux documents. Si les mots les plus fréquents dans les deux documents sont présents avec des fréquences similaires, le produit scalaire des vecteurs sera proche du maximum, à savoir le produit des longueurs des vecteurs. S’il n’y a pas de cooccurrence, le produit scalaire sera proche de zéro. Ici, l’objectif de la représentation vectorielle est la recherche d’information.
Les produits scalaires jouent également un rôle utile. Dans l’exemple ci-contre, deux documents contenant plusieurs des mêmes mots sont considérés comme similaires. Une façon de mesurer la co-occurrence de mots dans deux documents est de prendre le produit scalaire des vecteurs représentant les deux documents. Si les mots les plus fréquents dans les deux documents sont présents avec des fréquences similaires, le produit scalaire des vecteurs sera proche du maximum, à savoir le produit des longueurs des vecteurs. S’il n’y a pas de cooccurrence, le produit scalaire sera proche de zéro. Ici, l’objectif de la représentation vectorielle est la recherche d’information.
Après prétraitement des vecteurs de document, des requêtes sont formulées et nous souhaitons trouver pour chaque requête les documents les plus pertinents. Une requête est également représentée par un vecteur qui a un composant par mot; le composant mesure l’importance du mot pour la requête.
Prenons un exemple simple, à savoir, trouver des documents sur les voitures qui ne sont pas des voitures de course.
Un vecteur de requête aura une grande composante positive pour le mot voiture de même pour les mots moteur et peut-être une composante négative pour les mots course, parier, etc. Ici, les produits scalaires représentent la pertinence.
Un document dans une collection est pertinent s’il est similaire aux autres documents de la collection. Pour formaliser ceci, on peut définir une direction idéale pour une collection de vecteurs comme la ligne de meilleur ajustement, ou la ligne d’ajustement des moindres carrés, c’est-à-dire la ligne pour laquelle la somme des distances perpendiculaires au carré des vecteurs est minimisé. Ensuite, on peut classer les vecteurs en fonction de leur similitude de produit scalaire avec ce vecteur unitaire. Nous verrons que c’est une notion bien étudiée en algèbre linéaire et qu’il existe des algorithmes efficaces pour trouver la ligne de meilleur ajustement. Ainsi, ce classement peut être fait efficacement. Bien que la définition du rang semble ad hoc, elle donne d’excellents résultats dans la pratique et est devenue un outil de travail pour la recherche moderne, la recherche d’information et d’autres applications.

Notre but ici est de présenter au lecteur les fondements mathématiques pour traiter des données de grande dimension. Il y a deux parties importantes de ce fondement. Le premier est la géométrie à haute dimension avec les vecteurs, les matrices et l’algèbre linéaire.
Le deuxième aspect plus moderne est la combinaison avec la probabilité. Quand il y a un modèle stochastique avec des données de grande dimension, nous passons à l’étude des points aléatoires.
Encore une fois, il existe des modèles stochastiques détaillés spécifiques au domaine, mais en gardant notre objectif d’introduire les fondements, ces pages présentent au lecteur les résultats mathématiques nécessaires pour s’attaquer aux modèles stochastiques les plus simples, en supposant souvent des distributions indépendantes ou gaussiennes.
Propriétés des espaces à haute dimension
Notre intuition sur l’espace s’est formée en deux et trois dimensions et est souvent trompeuse dans les grandes dimensions. Pensez à placer 100 points uniformément au hasard dans un carré d’unité. Chaque coordonnée est générée indépendamment et uniformément au hasard à partir de l’intervalle [0, 1]. Sélectionnez un point et mesurez la distance à tous les autres points et observez la distribution des distances.
Augmentez ensuite la dimension et générez les points uniformément au hasard dans un cube unité de 100 dimensions. La distribution des distances se concentre autour d’une distance moyenne. La raison est facile à voir. Soit x et y deux points de ce genre dans d-dimensions. La distance entre x et y est
\)
