Au sens le plus large, la mécanique des fluides est l’étude des fluides au repos et en mouvement. Un fluide est défini comme n’importe quel matériau qui se déforme continuellement sous l’application d’une contrainte de cisaillement, dirigée tangentiellement à la surface du matériau. En d’autres termes, peu importe la force de la contrainte de cisaillement appliquée, ce fluide s’écoulera sous la contrainte appliquée (pour certains fluides, une limite d’élasticité doit être atteinte avant que le fluide ne s’écoule).
Certaines personnes définissent un fluide comme n’importe quel matériau qui prend la forme du récipient dans lequel il est maintenu. Il est facile de voir que n’importe quelle substance dans la phase liquide ou gazeuse réponderait à toutes ces définitions et est, par conséquent, celle des fluides. La distinction entre un fluide et un solide est également claire à partir de ces définitions parce que les solides ne prennent pas la forme de leurs conteneurs.
Si vous comparez l’action de solides et de fluides dans une condition de contrainte de cisaillement, la distinction est claire: un solide se déforme sous cisaillement, mais cette déformation ne se poursuit pas lorsque la force de cisaillement est retirée ou maintenue constante. Cependant, certains matériaux présentent des propriétés solides et fluides à la fois. Ces matériaux sont appelés matériaux « viscoélastiques », et ils se déforment continuellement sous une charge de cisaillement jusqu’à ce qu’une certaine déformation du seuil ait été atteinte. En fait, tous les matériaux solides réels doivent présenter certaines propriétés de fluide, mais les propriétés de type fluide peuvent être négligées dans la plupart des situations pratiques.
Nous commencerons notre discussion par un examen de la charge de cisaillement, qui devrait être familier dans le cadre de la mécanique solide. Une manière typique d’induire une charge de cisaillement sur un matériau solide est la torsion. elle apparait lorsque le matériau est chargé par des moments (ou des couples) qui produisent une rotation autour d’un axe à travers le matériau.
Dans les cours de mécanique des solides, l’analyse de torsion est généralement appliquée sur une barre fixe, fixée à une extrémité, et un moment (M) est appliqué à un endroit donné sur la longueur de la barre
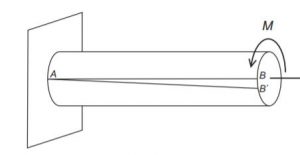
Par l’application d’un moment M sur l’axe horizontal, la ligne AB se déformera en arc de cercle $A$ $B_0$. Après suppression du moment, le point $B_0$ reviendrait à B, en supposant que la contrainte induite ne dépasse pas la limite d’élasticité des matériaux. Nous ne définirons pas ici les équations d’état appropriées pour cette condition de chargement.
