Introduction
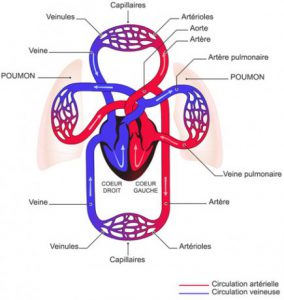Le système circulatoire forme une boucle fermée pour l’écoulement du sang qui transporte l’oxygène des poumons vers les tissus du corps et transporte le dioxyde de carbone des tissus vers les poumons . Il y a deux pompes pour surmonter la résistance et maintenir un débit constant. La partie gauche du cœur reçoit du sang riche en oxygène provenant des poumons et pompe ce sang dans le système artériel. Celui-ci forme un arbre de vaisseaux de plus en plus petits, commençant par l’aorte, se ramifiant aux petites artères, puis en artérioles et enfin en capillaires. L’échange de gaz a lieu dans les capillaires. En quittant le système capillaire , le sang entre dans le système veineux, à travers lesquelles il coule dans des vaisseaux de taille progressivement croissante vers la partie droite du coeur.
Le système veineux est constitué de veinules, de petites veines et de veines caves. La partie droite du cœur pompe le sang dans les artères pulmonaires, qui forment un arbre qui distribue le sang aux poumons. Les plus petites branches de cet arbre sont les capillaires pulmonaires, où le dioxyde de carbone sort et l’oxygène pénètre dans le sang. En quittant les capillaires pulmonaires, le sang oxygéné est recueilli par les veines pulmonaires, à travers lesquelles il retourne au cœur gauche. Il faut environ une minute pour qu’un globule rouge complète ce circuit.
Bien qu’il existe une symétrie structurelle apparente entre les circulations pulmonaire et systémique
, il existe des différences quantitatives significatives dans la pression et le volume sanguin. Néanmoins, la sortie des côtés droit et gauche du cœur doit toujours être à l’équilibre, même si le débit cardiaque, ou la quantité totale de sang pompée par le cœur, varie largement en fonction des besoins métaboliques du corps. L’un des objectifs de cette section est de comprendre comment le débit cardiaque est déterminé et régulé en réponse aux besoins métaboliques du corps. Des questions de cette nature ont été étudiées pendant de nombreuses années, et de nombreux livres ont été écrits sur le sujet (voir, par exemple, Guyton, 1963, ou Reeve et Guyton, 1967).
Des ouvrages plus récents ont été écrits par Ottensen sur les modéles mathématiques des systèmes circulatoires.
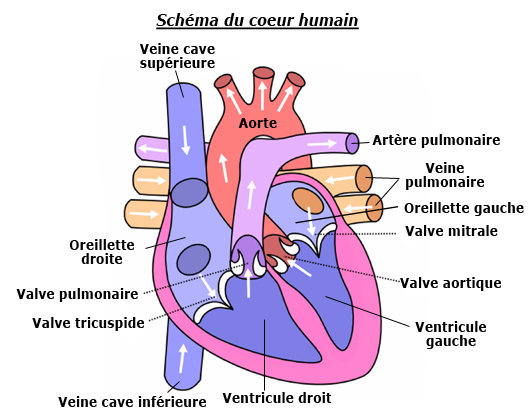
Chaque battement du cœur envoie une impulsion de sang à travers les artères, et la forme de ce pouls artériel change à mesure qu’il s’éloigne du cœur. Un problème intéressant est de comprendre ces changements et leur signification clinique en termes de propriétés du sang et des parois artérielles. Encore une fois, ce problème a été étudié en détail et nous ne présentons ici qu’un bref aperçu des modèles les plus anciens et les plus simples du pouls artériel.
Flux sanguin
Le terme tension artérielle se réfère à la force par unité de surface que le sang exerce sur les parois des vaisseaux sanguins. La pression artérielle varie à la fois dans le temps et la distance le long du système circulatoire. La pression systolique est la plus forte poussée de pression dans une artère, et résulte de l’éjection de sang par les ventricules pendant la contraction ventriculaire, ou systole.
La pression diastolique est la pression la plus basse atteinte pendant la relaxation ventriculaire et le remplissage, appelée diastole.
Dans l’aorte d’un humain normal, la pression systolique est d’environ 120 mm Hg et la pression diastolique est d’environ 80 mm Hg.
Si les effets de la gravité sont ignorés (ce que nous supposerons ici), alors on peut supposer que le sang coule uniquement en réponse aux gradients de pression. Le moyen le plus simple de caractériser un vaisseau sanguin est un vaisseau de résistance dans lequel le rayon est constant et le flux est linéairement proportionnel à la chute de pression.
Dans un récipient à résistance linéaire, le débit Q est lié à la pression par
| $$\bbox[white,8px] {Q=\frac{\Delta P}{R} \text{ où} \Delta \text{ P est la baisse de pression et R la résistance}} $$ |
La relation entre la résistance et le rayon du vaisseau est cruciale. Pour comprendre cette dépendance, supposons qu’un fluide visqueux se déplace lentement et régulièrement à travers un vaisseau cylindrique de rayon fixe.
La vitesse du fluide est décrite par un vecteur u qui a des composantes axiales, radiales et angulaires. Comme le fluide est incompressible et conservé, il est possible d’écrire:
| $$\bbox[white,8px] {\nabla . \bf u = 0 } $$ |
De plus, comme la quantité de moment est conservé, l’équation de Navier-Stokes peut être appliquée.
| $$\bbox[white,8px] {\rho(\bf u_t + \bf u.\nabla \bf u)= – \nabla P + \mu \nabla^2 \bf u } $$ |
Si le flux est considéré stable et les termes non linéaires faibles par rapport à la viscosité, alors on peut écrire :
| $$\bbox[white,8px] { \mu \nabla^2 \bf u = \nabla P } $$ |
Cette simplification de l’équation de Navier-Stokes donne l’équation de Stokes.
L’applicabilité de l’équation de Stokes au flux sanguin est suspecte pour plusieurs raisons :
- La contribution de la viscosité (via le laplacien $\nabla$) dans l’équation de Stokes est dérivée d’une loi de comportement supposée relier les contraintes et les déformations du fluide (Segel, 1977). Or cette loi est connue pour ne pas convenir pour des fluides contenant de longs polymères ou d’autres structures chimiques compliquées.
- Dans les capillaires, la grande taille des globules rouges par rapport au diamètre typique d’un capillaire suggère qu’une description du continuum n’est pas appropriée.
Cependant, nous ne nous occupons pas de ces questions et acceptons la description de l’équation de Stokes comme adéquate.
Nous cherchons une solution de l’équation de Stokes dont la seule composante non nulle est la composante axiale. Nous définissons les coordonnées sur le cylindre de la manière habituelle, x étant la distance le long du cylindre dans la direction axiale et r la direction radiale. La direction angulaire, avec la coordonnée θ, n’entre pas en compte dans cette analyse.
Si l’on considère le seul flux axial, la condition d’incompressibilté permet d’écrire $$\dfrac{\partial u}{\partial x}=0$$ où u est le compsant axial du vecteur vitesse. Ainsi u est indépendant de x.
Dans le cas d’un fluide continu, l’équation de Stokes peut s’écrire :
| $$\bbox[white,8px] {\mu \dfrac{1}{r} \dfrac{d}{dr} (r \dfrac{d}{dr} u ) = \dfrac{d P}{dx} = P_x} $$ |