L’analyse théorique et la modélisation computationnelle sont des outils importants pour caractériser ce que font les systèmes nerveux, déterminer leur fonctionnement et comprendre pourquoi ils fonctionnent de manière particulière. La neuroscience englobe des approches allant des études moléculaires et cellulaires à la psychophysique humaine et à la psychologie. Les neurosciences théoriques encouragent la diaphonie entre ces sous-disciplines en construisant des représentations compactes de ce qui a été appris, en établissant des ponts entre différents niveaux de description et en identifiant des concepts et des principes unifiants. Dans ce livre, nous présentons les méthodes de base utilisées à ces fins et discutons des exemples dans lesquels les approches théoriques ont donné un aperçu de la fonction du système nerveux.
Les questions quoi, comment et pourquoi sont abordées par des modèles descriptifs, mécanistes et interprétatifs, dont nous traitons chacun dans les chapitres suivants. Les modèles descriptifs résument de grandes quantités de données expérimentales de manière compacte mais précise, caractérisant ainsi ce que font les neurones et les circuits neuronaux. Ces modèles peuvent être vaguement basés sur des résultats biophysiques, anatomiques et physiologiques, mais leur but premier est de décrire les phénomènes, pas de les expliquer. D’autre part, les modèles mécanistes abordent la question de savoir comment les systèmes nerveux fonctionnent sur la base de l’anatomie, de la physiologie et des circuits connus. De tels modèles forment souvent un pont entre les modèles descriptifs formulés à différents niveaux. Les modèles interprétatifs utilisent des principes computationnels et théoriques de l’information pour explorer la signification comportementale et cognitive de divers aspects de la fonction du système nerveux, abordant la question de savoir pourquoi les systèmes nerveux fonctionnent comme ils le font.
Il est souvent difficile d’identifier le niveau de modélisation approprié pour un problème particulier. Une erreur fréquente consiste à supposer qu’un modèle plus détaillé est nécessairement supérieur. Parce que les modèles agissent comme des ponts entre les niveaux de compréhension, ils doivent être suffisamment détaillés pour entrer en contact avec le niveau inférieur, mais assez simple pour fournir des résultats clairs au niveau supérieur.
Ce livre est organisé en trois parties sur la base de thèmes généraux.
La partie I, Encodage neuronal et décodage, (chapitres 1 à 4) est consacrée au codage de l’information par les potentiels d’action et la représentation de l’information par les populations de neurones à réponses sélectives.
La modélisation des neurones et des circuits neuronaux sur la base de la biophysique cellulaire et synaptique est présentée dans la partie II, Neurones et circuits neuronaux (chapitres 5 à 7).
Le rôle de la plasticité dans le développement et l’apprentissage est discuté dans la partie III, Adaptation et apprentissage (chapitres 8-10). À l’exception des chapitres 5 et 6, qui couvrent conjointement la modélisation neuronale, les chapitres sont largement indépendants et peuvent être choisis et classés de diverses façons pour un cours d’un ou de deux semestres au premier cycle ou au deuxième cycle.
Bien que nous fournissions du matériel de base, les lecteurs sans expérience préalable en neurosciences devraient se référer à un manuel de neurosciences tel que Kandel, Schwartz et Jessell (2000); Nicholls, Martin et Wallace (1992); Bear, Connors et Paradiso (1996); Shepherd (1997); Zigmond et al. (1998); ou Purves et al. (2000).
La neuroscience théorique est basée sur la croyance que les méthodes des mathématiques, de la physique et de l’informatique peuvent fournir des informations importantes sur la fonction du système nerveux. Malheureusement, les mathématiques peuvent parfois sembler plus un obstacle qu’une aide à la compréhension. Nous n’avons pas hésité à utiliser le niveau d’analyse nécessaire pour être précis et rigoureux. Parfois, cela peut étirer la tolérance de certains de nos lecteurs. Nous encourageons ces lecteurs à consulter l’Annexe mathématique, qui fournit un bref aperçu de la plupart des méthodes mathématiques utilisées dans le texte, mais aussi de persévérer et tenter de comprendre les implications et les conséquences d’une dérivation difficile même si ses étapes ne sont pas claires.
Encodage et décodage neuronal
Encodage neuronal I: taux de déclenchement et statistiques de pointe
Introduction
- Le système nerveux comporte deux divisions principales,
- Le système nerveux central (SNC)
- Le système nerveux périphérique (SNP)
- Dans le SNC, composé de l’encéphale et de la moelle épinière, ont lieu
- l’intégration et la corrélation de diverses sortes d’informations sensorielles entrantes,
- la génération des pensées et des émotions,
- la formation et le stockage des souvenirs.
De plus, la plupart des influx nerveux qui stimulent la contraction musculaire et la sécrétion glandulaire proviennent du SNC.
Le SNP peut être subdivisé, d’après la partie du corps qui réagit, en
- système nerveux somatique (sôma: corps) (SNS)
- et en système nerveux autonome (SNA),
Les neurones
- Certains neurones sont minuscules et transmettent des signaux sur une courte distance (moins de 1 mm) dans le SNC.
- D’autres sont les cellules les plus longues du corps.
- Ainsi, les neurones moteurs qui commandent à des muscles de remuer un orteil s’étendent depuis la région lombaire de la moelle épinière (juste au-dessus de la taille) jusqu’au pied.
-
Une synapse est le contact fonctionnel entre deux neurones ou entre un neurone et une cellule effectrice (musculaire ou glandulaire).
-
Elle est appelée jonction neuromusculaire, entre un neurone moteur et une fibre musculaire, et jonction neuro-glandulaire, entre un neurone et une cellule glandulaire.
Les parties d’un neurone
- La plupart des neurones se composent de trois grandes parties: le corps cellulaire, les dendrites et l’axone
-
Le corps cellulaire (soma ou péricaryon) renferme un noyau entouré de cytoplasme qui comprend des organites types, tels que des lysosomes, des mitochondries et un appareil de Golgi.
- Les neurofîbrilles, composées de filaments intermédiaires, forment le cytosquelette qui assure soutien et forme à la cellule.
- Les neurones possèdent deux sortes de prolongements : les dendrites et les axones
- La dendrite (dendron : arbre) est habituellement courte, effilée et bien ramifiée.
- Elle présente souvent un déploiement de prolongements qui a la forme d’un arbre.
- Ces derniers émergent du corps cellulaire.
- En général, la dendrite est non myélinisée.
-
L’axone, prolongement long, fin et cylindrique qui peut être myélinisé, s’unit au corps cellulaire au niveau d’une élévation de forme conique, appelée cône d’implantation de l’axone.
-
La première partie de l’axone est appelée segment initial.
- À l’exception des neurones sensitifs, les influx nerveux se produisent à la jonction du cône et du segment initial appelée zone gâchette, puis sont conduits le long de l’axone vers un neurone, une fibre musculaire ou une cellule glandulaire.
- Son cytoplasme, l’axoplasme, est entouré d’une membrane plasmique appelée axolemme (lemma: gaine).
- Sur la longueur d’un axone, des branches appelées collatérales d’axone peuvent être présentes, en général à angle droit par rapport à l’axone.
- L’axone et ses collatérales se terminent en se divisant en de nombreux prolongements minces appelés terminaisons axonales.
Le transport axonal
- Le corps cellulaire d’un neurone est le site de la plupart des réactions de synthèse et du recyclage des molécules usées en nouveaux composants.
- Toutefois, certaines substances sont nécessaires dans l’axone ou aux terminaisons axonales.
- Des systèmes de transport, de 2 sortes, déplacent des particules depuis le corps cellulaire jusqu’à ces terminaisons et vice versa.
Le transport axonal lent
- Le transport axonal (flux axoplas-mique) lent, déplace les particules d’environ 1 à 5 mm par jour.
- Il véhicule l’axoplasme dans une seule direction, soit depuis le corps cellulaire jusqu’aux terminaisons axonales.
- Il fournit du nouvel axoplasme destiné au développement ou à la régénération des axones et renouvelle l’axoplasme dans les axones matures et en croissance.
-
Le transport axonal rapide déplace les particules à la vitesse approximative de 200 à 400 mm par jour.
-
Il utilise des «moteurs» moléculaires afin de transporter des particules dans les deux directions, soit en dehors du corps cellulaire et vers celui-ci, le long de la surface des microtubules.
Le transport axonal rapide
- Il véhicule divers organites et matériaux qui forment les membranes de l’axolemme, des boutons synaptiques et des vésicules synaptiques.
- Des particules qui retournent vers le corps cellulaire sont dégradées ou recyclées, alors que d’autres influent sur la croissance de ce dernier.
- D’autres encore, telles que certains virus, peuvent même nuire au corps cellulaire.
La classification des neurones
- Les différents neurones du corps sont classés selon leur structure et leur fonction.
- La classification structurale tient compte du nombre de prolongements partant du corps cellulaire.
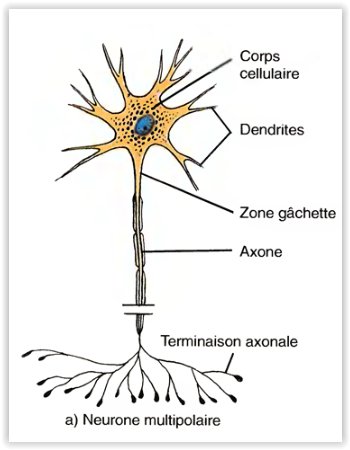
Les neurones multipolaires
- Possèdent généralement un certain nombre de dendrites et un axone . La plupart des neurones dans l’encéphale et dans la moelle épinière sont de ce type.
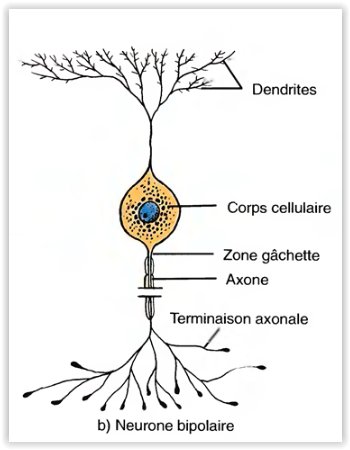
Les neurones bipolaires
- Ont une dendrite et un axone.
- Ils se trouvent dans la rétine, l’oreille interne et l’aire olfactive de l’encéphale.
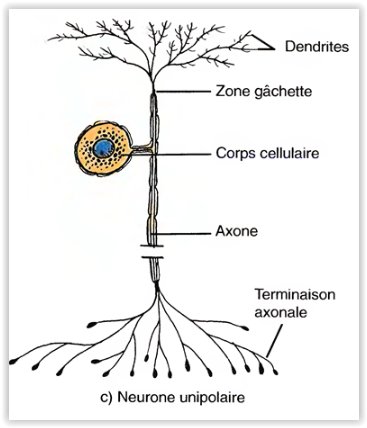
Les neurones unipolaires
- (pseudo-unipolaires) sont dotés d’un seul prolongement issu du corps cellulaire.
- Ce sont toujours des neurones sensitifs.
- La classification fonctionnelle tient compte du sens de propagation de l’influx nerveux.
-
Les neurones afférents:
- transmettent des influx nerveux sensoriels depuis des récepteurs situés dans la peau, les organes des sens, les muscles, les articulations et les viscères jusqu’à l’encéphale et à la moelle épinière.
-
Les neurones efférents:
- véhiculent les influx nerveux moteurs depuis l’encéphale et la moelle épinière jusqu’aux effecteurs, soit les muscles ou les glandes.
- Les neurones d’association, ou interneurones:
- transmettent les influx nerveux d’un neurone à un autre.
- La plupart (90 %) des neurones du corps sont des neurones d’association.
- Les nerfs rachidiens et crâniens contiennent des fibres qui relèvent de sept catégories fonctionnelles, soit quatre afférentes et trois efférentes.
la neurophysiologie
- La communication par neurones dépend de deux propriétés fondamentales de leur membrane plasmique.
- En premier lieu, il existe une tension électrique appelée potentiel de repos membranaire à travers la membrane.
- En second lieu, leur membrane plasmique contient divers canaux ioniques (pores) qui peuvent être ouverts ou fermés.
-
Si ces derniers sont ouverts, des ions spécifiques situés dans le liquide intracellulaire (cytosol) ou extracellulaire peuvent traverser la membrane.
-
Une partie de la protéine qui forme ce canal peut agir comme une barrière ou comme une porte et s’ouvrir ou se fermer sur demande.
-
Selon les types de canaux présents, une partie d’un neurone peut produire soit des potentiels gradués soit des potentiels d’action (influx nerveux).
le potentiel de repos membranaire
- Le potentiel de repos membranaire résulte d’une faible accumulation de charges négatives sur la face interne de la membrane et d’une égale accumulation de charges positives sur la face externe .
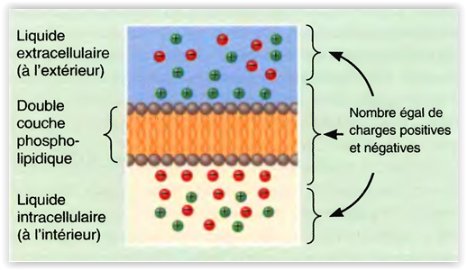
- Cette séparation de charges électriques positives et négatives constitue une forme d’énergie potentielle mesurée en volts ou en millivolts (1 mV = 1/1000 V).
- Plus la différence de charge de part et d’autre de la membrane est importante, plus le potentiel de membrane (la tension) est élevé(e).
-
Dans les neurones, le potentiel de repos varie entre -40 et -90 mV. La valeur usuelle est de -70 mV.
-
Le signe moins signifie que la charge est négative à l’intérieur par rapport à l’extérieur.
-
Une cellule qui présente un potentiel de membrane est dite polarisée.
-
La plupart des cellules corporelles sont polarisées, et la tension de la membrane varie entre +5 mV et -100 mV dans divers types de cellules.
-
Le potentiel de repos ressemble au voltage d’une batterie.
-
Si l’on relie les bornes positive et négative de celle-ci avec un fil métallique, un flux d’électrons passe le long du fil.
-
Le flux de charge électrique est appelé le courant.
-
Dans une cellule vivante, les ions plutôt que les électrons transportent la majeure partie du courant.
- Vu que la double couche phospholipidique de la membrane plasmique est un bon isolant, les principales voies réservées au flux de courant à travers la membrane se trouvent dans les canaux ioniques.
- Donc, lorsque ces derniers s’ouvrent ou se ferment dans la membrane plasmique, un flux de courant se produit, ce qui change le potentiel de membrane.
-
Il existe deux facteurs principaux qui contribuent au potentiel de repos membranaire.
- La répartition d’ions à travers la membrane plasmique. Les principaux anions et cations sont différents à l’extérieur et à l’intérieur de la cellule. Le liquide extracellulaire est riche en Na+ et en CL-. En revanche, dans le liquide intracellulaire, le principal cation est K+ et les deux anions dominants sont les phosphates organiques et les acides aminés dans les protéines.
- La perméabilité relative de la membrane plasmique au Na+ et au K+. La perméabilité de la membrane plasmique au K+ est de 50 à 100 fois supérieure à celle du Na+ dans un neurone ou une fibre musculaire, au repos.
Les canaux ioniques
- Il existe deux principaux types de canaux ioniques ;
- Les canaux de fuite sont toujours ouverts,
- Alors que les canaux à ouverture périodique s’ouvrent et se ferment en réaction à une certaine sorte de stimulus.
- Vu que la membrane plasmique d’un neurone ou d’une fibre musculaire possède plus de canaux de fuite K+ que de canaux de fuite Na+, la perméabilité de la membrane au K+ est plus élevée.
- 4 catégories de stimuli font actionner les canaux ioniques à ouverture périodique :
- la tension,
- les produits chimiques,
- la pression mécanique
- et la lumière.
- Le premier type de canal ionique à ouverture périodique, appelé canal ionique voltage-dépendant (réglé par la tension), s’ouvre en réaction à une modification directe du potentiel (de la tension) de la membrane.
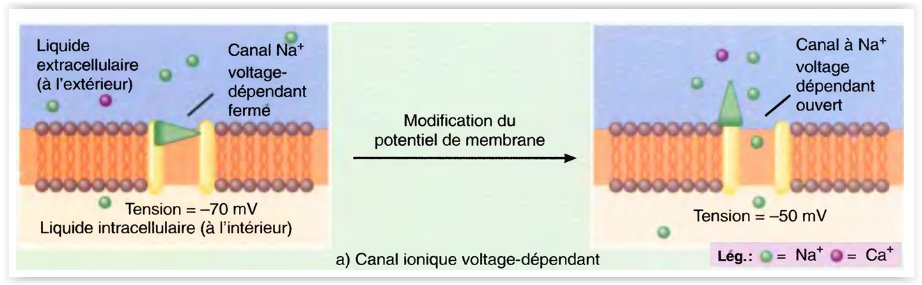
- La présence de ces canaux dans les membranes plasmiques des nerfs et des muscles donne à ces cellules la propriété d’excitabilité (d’irritabilité), c’est-à-dire la possibilité de réagir à certains stimuli par la production d’influx nerveux.
-
La zone gâchette d’un neurone donné se trouve là où, sur la membrane, les canaux voltage-dépendants sont plus abondamment groupés.
- Les canaux ioniques chimiquement dépendants s’ouvrent et se ferment, en réaction à un certain stimulus chimique.
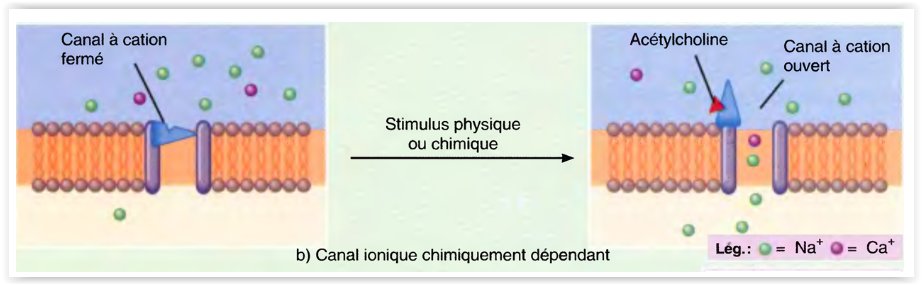
- Une grande diversité de ligands chimiques, tels que les neurotransmetteurs, les hormones et les ions tels que H+ et Ca2+, règlent ces canaux.
-
Ainsi, le neurotransmetteur qu’est l’acétylcholine ouvre les canaux à cation qui font passer Na+, K+ et Ca+.
-
Les canaux ioniques chimiquement dépendants fonctionnent de deux façons principales.
-
Le produit chimique peut directement modifier la perméabilité de la membrane à un ou à plus d’un ion, comme dans l’exemple de l’acétylcholine.
-
Autrement, il peut agir indirectement par l’intermédiaire aussi bien d’un type de protéine de la membrane appelé protéine G que d’un système de second messager qui utilise des molécules contenues dans le cytosol.
-
Les hormones, de même que certains neurotransmetteurs, fonctionnent souvent par systèmes de seconds messagers.
Potentiel d’action (influx nerveux) dans un neurone
- Les canaux ioniques mécaniquement dépendants s’ouvrent ou se ferment, en réaction à une pression ou à une vibration mécanique telle que le toucher ou des ondes sonores.
- Finalement, les canaux ioniques réglés par la lumière se ferment en réaction à la lumière.
- Ces deux types de canaux se trouvent dans les récepteurs sensoriels qui décèlent les distorsions mécaniques ou la lumière.
- La présence de canaux ioniques réglés chimiquement, mécaniquement ou par la lumière dans une membrane permet au stimulus approprié de provoquer la formation d’un potentiel gradué.
- Ces réactions électriques varient en importance.
- Elles sont plus grandes ou plus petites selon aussi bien le nombre de canaux ioniques à ouverture périodique qui se sont ouverts que leur durée d’ouverture.
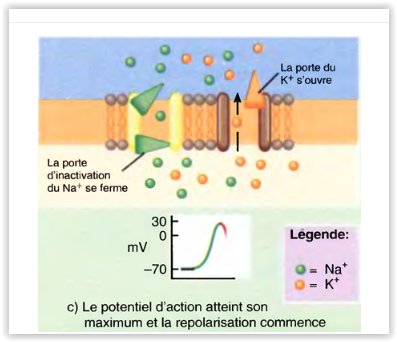
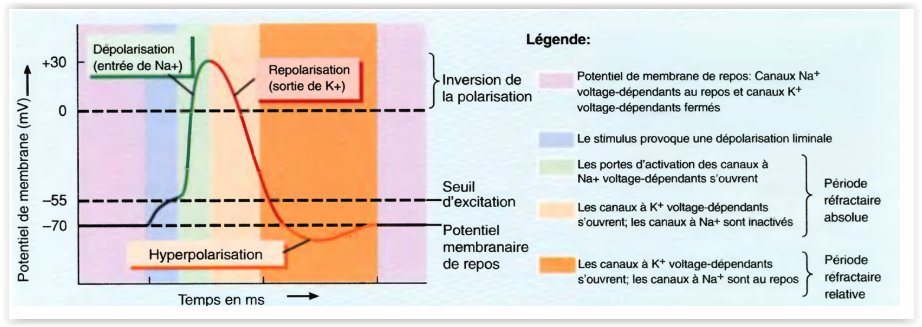
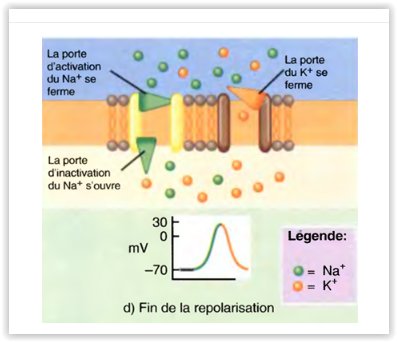
Modifications constatées dans les canaux voltage-dépendants pendant la dépolarisation et la repolarisation du potentiel d’action
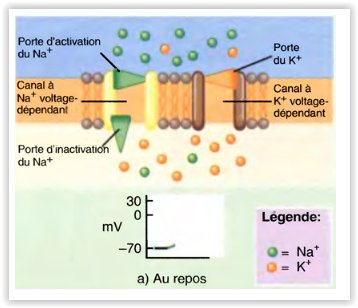
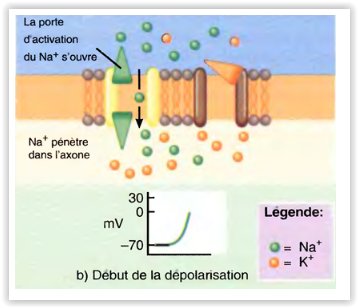
La repolarisation commence.
La transmission aux synapses
- Les synapses permettent d’intégrer et de filtrer l’information.
- Certains signaux sont transmis, alors que d’autres sont bloqués.
- Certaines maladies cérébrales et de nombreuses maladies mentales découlent d’une interruption de la communication synaptique.
- C’est aussi aux synapses qu’agissent de nombreux médicaments qui affectent l’encéphale.
- Ces derniers comprennent les substances thérapeutiques et les drogues.
- Il existe deux types de synapses:
- électriques
- chimiques,
Les synapses électriques
- Dans une synapse électrique, le courant ionique passe directement d’une cellule à une autre, à travers les jonctions lacunaires.
-
Chacune de ces dernières contient près d’une centaine de structures protéiques tubulaires appelées connexons qui forment des tunnels destinés à relier le cytosol des deux cellules ; le flux de courant ionique emprunte cette voie.
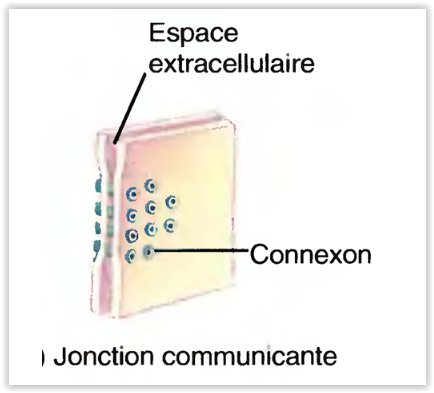
Les synapses électriques comportent deux avantages :
- Elles permettent la communication plus rapidement que les synapses chimiques, vu que les influx traversent les jonctions lacunaires,
- Elles peuvent synchroniser l’activité d’un groupe de neurones ou de fibres musculaires. L’utilité des potentiels d’action synchronisés dans le muscle lisse cardiaque ou viscéral est de produire la contraction coordonnée de ces fibres. Dans le SNC, le rôle des synapses électriques reste encore à découvrir.
Les synapses chimiques
- Même si les neurones présynaptiques et postsynaptiques d’une synapse chimique sont proches, leurs membranes ne se touchent pas.
- Ces dernières sont séparées par la fente synaptique, un espace de 20- à 50-nm rempli de liquide extracellulaire.
- Même si les neurones présynaptiques et postsynaptiques d’une synapse chimique sont proches, leurs membranes ne se touchent pas.
- Ces dernières sont séparées par la fente synaptique, un espace de 20- à 50-nm rempli de liquide extracellulaire
Les neurones sont remarquables parmi les cellules du corps dans leur capacité à propager des signaux rapidement sur de grandes distances. Ils le font en générant des impulsions électriques caractéristiques appelées potentiels d’action ou, plus simplement, des pointes qui peuvent voyager dans les fibres nerveuses. Les neurones représentent et transmettent des informations en tirant des séquences de pointes dans divers modèles temporels.
L’étude du codage neural, qui fait l’objet des quatre premiers chapitres de ce livre, consiste à mesurer et caractériser comment les attributs du stimulus, tels que l’intensité lumineuse ou sonore, ou les actions motrices, comme la direction d’un mouvement du bras, sont représentés par Potentiels d’action.
Le lien entre le stimulus et la réponse peut être étudié de deux points de vue opposés. L’encodage neuronal, sujet des chapitres 1 et 2, fait référence à la carte du stimulus à la réponse. Par exemple, nous pouvons cataloguer comment les neurones réagissent à une grande variété de stimuli, puis construire des modèles qui tentent de prédire les réponses à d’autres stimuli. Le décodage neuronal fait référence à la carte inverse, de la réponse au stimulus, et le défi consiste à reconstruire un stimulus, ou certains aspects de ce stimulus, à partir des séquences de pointes qu’il évoque. Le décodage neural est discuté au chapitre 3. Dans le chapitre 4, nous examinons comment la quantité d’informations codées par des séquences de potentiels d’action peut être quantifiée et maximisée. Avant d’entamer cette tournée de codage neuronal, nous passons brièvement en revue comment les neurones génèrent leurs réponses et comment l’activité neuronale est enregistrée. Les mécanismes biophysiques sous-jacents aux réponses neuronales et à la génération de potentiel d’action sont traités plus en détail dans les chapitres 5 et 6.
Propriétés des neurones
Les neurones sont hautement spécialisés pour générer des signaux électriques en réponse à des intrants chimiques et autres, et les transmettre à d’autres cellules. Certaines spécialisations morphologiques importantes, vues dans la figure 1.1, sont les dendrites qui reçoivent des intrants d’autres neurones et l’axone qui transporte la sortie neuronale vers d’autres cellules. La structure branchée complexe de l’arbre dendritique permet à un neurone de recevoir des intrants de nombreux autres neurones via des connexions synaptiques. Le neurone pyramidal cortical de la figure 1.1A et l’interneurone cortical de la figure 1.1C reçoivent chacun des milliers d’entrées synaptiques, et pour la cellule de Purkinje cérébelleuse de la figure 1.1B, le nombre est supérieur à 100.000. La figure 1.1 ne montre pas l’étendue complète des axones de ces neurones. Les axones provenant de neurones uniques peuvent traverser de grandes fractions du cerveau ou, dans certains cas, du corps entier. Dans le cerveau de la souris, il a été estimé que les neurones corticaux envoient généralement un total d’environ 40 mm d’axone et ont environ 10 mm de dendritique totale câble dans leurs arbres dendritiques ramifiés. L’axone fait une moyenne de 180 connexions synaptiques avec d’autres neurones par mm de longueur et le dendritique arbre reçoit, en moyenne, 2 entrées synaptiques par μm. Le corps cellulaire ou soma d’un neurone cortical typique varie de diamètre d’environ 10 à 50 μm.
Parallèlement à ces caractéristiques morphologiques, les neurones ont des spécialisations physiologiques. Les plus importants d’entre eux sont une grande variété de membranes qui permettent aux ions, principalement le sodium (Na +), le potassium (K +), le calcium (Ca2 +) et le chlorure (canaux ioniques Cl-), d’entrer et de sortir de la cellule. Les canaux ioniques contrôlent le flux d’ions à travers la membrane cellulaire en s’ouvrant et se fermant en réponse aux changements de tension et aux signaux internes et externes.
Le signal électrique intéressant le système nerveux est la différence de potentiel électrique entre l’intérieur d’un neurone et le milieu extracellulaire environnant. Dans des conditions de repos, le potentiel à l’intérieur de la membrane cellulaire d’un neurone est d’environ -70 mV par rapport à celui du bain environnant (qui est classiquement défini comme étant de 0 mV), et la cellule est dite polarisée. Les pompes à ions situées dans la membrane cellulaire maintiennent des gradients de concentration qui supportent cette différence de potentiel membranaire.
Par exemple, Na + est beaucoup plus concentré à l’extérieur d’un neurone qu’à l’intérieur, et la concentration de K + est significativement plus élevée à l’intérieur du neurone que dans le milieu extracellulaire. Les ions circulent ainsi dans et hors d’une cellule en raison des gradients de tension et de concentration. Le courant sous la forme d’ions chargés positivement sortant de la cellule (ou des ions chargés négativement s’écoulant dans la cellule) à travers des canaux ouverts rend le potentiel de la membrane plus négatif, un processus appelé hyperpolarisation. L’abaissement du courant dans la cellule change le potentiel de la membrane en valeurs moins négatives ou même positives. C’est ce qu’on appelle la dépolarisation.
Si un neurone est suffisamment dépolarisé pour élever le potentiel membranaire au-dessus d’un niveau seuil, un processus de rétroaction positive est initié et le neurone génère un potentiel d’action. Un potentiel d’action est une fluctuation d’environ 100 mV du potentiel électrique à travers la membrane cellulaire qui dure environ 1 ms (figure 1.2A). La génération de potentiel d’action dépend également de l’histoire récente du tir de cellules. Pendant quelques millisecondes, juste après l’activation d’un potentiel d’action, il peut être pratiquement impossible d’amorcer un autre pic. C’est ce qu’on appelle la période réfractaire absolue. Pour un intervalle plus long, connu sous le nom de période réfractaire relative, qui dure jusqu’à des dizaines de millisecondes après un pic, il est plus difficile d’évoquer un potentiel d’action.
Les potentiels d’action sont d’une grande importance car ils sont la seule forme de fluctuation potentielle de la membrane qui peut se propager sur de grandes distances.
Les fluctuations potentielles inférieures au seuil sont sévèrement atténuées sur des distances de 1 mm ou moins. D’autre part, les potentiels d’action sont régénérés activement le long des processus axonaux et peuvent se déplacer rapidement sur de grandes distances sans atténuation.
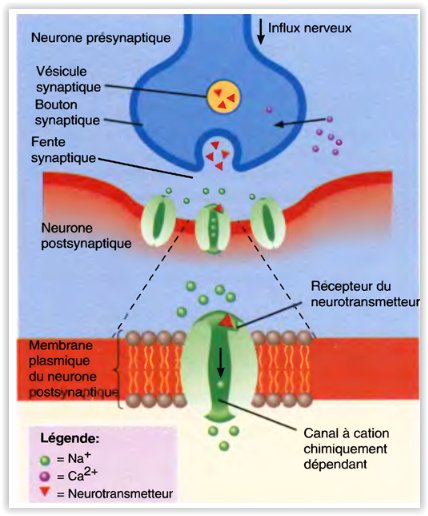
Les axones se terminent aux synapses où la tension transitoire du potentiel d’action ouvre les canaux ioniques, produisant un influx de Ca2 + qui conduit à la libération d’un neurotransmetteur (figure 1.2B). Le neurotransmetteur se lie aux récepteurs du côté receveur du signal ou post-synaptique de la synapse, provoquant l’ouverture des canaux conducteurs d’ions. Selon la nature du flux d’ions, les synapses peuvent avoir un effet excitateur, dépolarisant ou inhibiteur, typiquement hyperpolarisant, sur le neurone postsynaptique.
Enregistrement des réponses neuronales
La figure 1.3 illustre des méthodes intracellulaires et extracellulaires pour enregistrer les réponses neuronales électriquement (elles peuvent également être enregistrées optiquement).
Les potentiels membranaires sont mesurés de manière intracellulaire en connectant une électrode de verre creuse remplie d’un électrolyte conducteur à un neurone, et en comparant le potentiel qu’il enregistre avec celui d’une électrode de référence placée dans le milieu extracellulaire. Les enregistrements intracellulaires sont faits soit avec des électrodes pointues insérées à travers la membrane dans la cellule, ou des électrodes de patch qui ont des pointes plus larges et sont scellés hermétiquement à la surface de la membrane. Après le scellement de l’électrode de patch, la membrane située sous son extrémité est cassée ou perforée, fournissant un contact électrique avec l’intérieur de la cellule. La trace supérieure de la figure 1.3 est un schéma d’un enregistrement intracellulaire provenant du soma d’un neurone tirant une séquence de potentiels d’action.
L’enregistrement montre des pointes rapides qui chevauchent un potentiel subthreshold variant plus lentement. La trace inférieure est un schéma d’un enregistrement intracellulaire fait une certaine distance sur l’axone du neurone.
Ces traces sont des dessins, pas de vrais enregistrements; de tels enregistrements axonaux intracellulaires, bien que possibles dans certains types de cellules, sont difficiles et rares. Les enregistrements intracellulaires du soma sont la norme, mais les enregistrements dendritiques intracellulaires sont de plus en plus réalisés. La forme d’onde du potentiel membranaire sous-seuil, apparente dans l’enregistrement du soma, est complètement absente sur l’axone en raison de l’atténuation, mais la séquence du potentiel d’action dans les deux enregistrements est la même. Ceci illustre le point important que les pointes, mais pas les potentiels infraliminaires, propagent régénérativement les axones.
La trace médiane de la figure 1.3 illustre un enregistrement extracellulaire idéalisé et sans bruit. Ici, une électrode est placée près d’un neurone mais elle ne pénètre pas dans la membrane cellulaire. De tels enregistrements peuvent révéler les potentiels d’action déclenchés par un neurone, mais pas ses potentiels membranaires inférieurs au seuil. Les enregistrements extracellulaires sont généralement utilisés pour des expériences in vivo, en particulier celles impliquant des animaux se comportant. Les enregistrements intracellulaires sont parfois faits in vivo, mais c’est difficile à faire. L’enregistrement intracellulaire est plus couramment utilisé pour des préparations in vitro, telles que des tranches de tissu neural.
Les réponses étudiées dans ce chapitre sont des séquences potentielles d’action qui peuvent être enregistrées soit intra soit extracellulairement.
De la stimulation à la réponse
Caractériser la relation entre le stimulus et la réponse est difficile car les réponses neuronales sont complexes et variables. Les neurones réagissent généralement en produisant des séquences de pic complexes qui reflètent à la fois la dynamique intrinsèque du neurone et les caractéristiques temporelles du stimulus.
Il peut être difficile d’isoler les caractéristiques de la réponse qui codent les changements dans le stimulus, surtout si l’échelle de temps pour ces changements est du même ordre que l’intervalle moyen entre les pics. Les réponses neuronales peuvent varier d’un essai à l’autre, même si le même stimulus est présenté de façon répétée.
Il existe de nombreuses sources potentielles de cette variabilité, y compris des niveaux variables d’excitation et d’attention, un caractère aléatoire associé à divers processus biophysiques affectant le déclenchement neuronal, et les effets d’autres processus cognitifs intervenant au cours d’un essai. La complexité et la variabilité d’essai à essai des séquences potentielles d’action rendent improbable la possibilité de décrire et de prédire le moment de chaque pic de façon déterministe. Au lieu de cela, nous cherchons un modèle qui peut expliquer les probabilités que différentes séquences de pointes sont évoquées par un stimulus spécifique.
Typiquement, de nombreux neurones répondent à un stimulus donné, et les caractéristiques du stimulus sont donc codées par les activités de grandes populations neurales. En étudiant le codage de population, nous devons examiner non seulement les modèles de tir des neurones individuels, mais aussi les relations de ces modèles de tir les uns aux autres à travers la population des cellules répondantes.
Dans ce chapitre, nous introduisons les fonctions de corrélation entre le taux de tir et le rapport spike-train, qui sont des mesures de base de la probabilité de dopage et des statistiques.
Nous discutons également du moyennage déclenché par pic, une méthode pour relier les potentiels d’action au stimulus qui les a provoqués. Enfin, nous présentons des descriptions stochastiques de base de la génération de pointes, les modèles de Poisson homogènes et inhomogènes, et nous discutons d’un modèle simple de réponses neuronales auxquelles elles conduisent. Dans le chapitre 2, nous continuons notre discussion sur le codage neural en montrant comment les méthodes de corrélation inverse sont utilisées pour construire des estimations des taux d’allumage en réponse à des stimuli variables dans le temps.
Ces méthodes ont été largement appliquées aux réponses neurales dans la rétine, le noyau géniculé latéral (LGN) du thalamus et le cortex visuel primaire, et nous examinons les modèles résultants.
Les potentiels d’action transmettent l’information à travers leur timing. Bien que les potentiels d’action puissent varier quelque peu en durée, en amplitude et en forme, ils sont généralement traités comme des événements stéréotypés identiques dans les études de codage neuronal. Si nous ignorons la courte durée d’un potentiel d’action (environ 1 ms), une séquence potentielle d’action peut être caractérisée simplement par une liste des moments où des pointes se sont produites. Pour n pointes, nous notons ces temps par ti avec i = 1, 2, …, n. L’essai au cours duquel les pics sont enregistrés est pris pour commencer à l’instant 0 et se terminer à l’instant T, donc 0 ≤ $t_i$ ≤ T pour tout i. La séquence de pointes peut également être représentée comme une somme de pointes idéalisées, infinitésimales, sous la forme de fonctions de Dirac $\delta$ (voir l’Annexe Mathématique),
| $$\bbox[white,8px] {\rho (t) = \sum_{i=1}^{i=n} \delta (t – t_i)} \label{ref1}$$ |
Nous appelons $\rho (t)$ la fonction de réponse neurale et l’utilisons pour ré-exprimer des sommes sur des pointes comme des intégrales dans le temps. Par exemple, pour toute fonction $h(t)$, nous pouvons écrire
| $$\bbox[white,8px] {\sum_{i=1}^{i=n} h(t – t_i) = \int_{-\infty}^{+\infty} {d\tau h(\tau) \rho (t-\tau)}} \label{ref2}$$ |
où l’intégrale est sur la durée de l’essai. L’égalité découle de l’équation de définition de base pour une fonction $\delta$, à condition que les limites de l’intégrale entourent le point $t$ (si ce n’est pas le cas, l’intégrale est égale à 0).
| $$\bbox[white,8px] {\int{d\tau h(\tau) \rho (t-\tau) = h(t)}} \label{ref3}$$ |
Comme la séquence des potentiels d’action générés par un stimulus donné varie d’un essai à l’autre, les réponses neuronales sont généralement traitées statistiquement ou de façon probabiliste. Par exemple, ils peuvent être caractérisés par des vitesses d’allumage, plutôt que par des séquences de pointes spécifiques. Malheureusement, le terme « taux de rendement » est appliqué de manière classique à un certain nombre de quantités différentes. Le plus simple d’entre eux est ce que nous appelons le taux de comptage des pointes, qui est obtenu en comptant le nombre de potentiels d’action qui apparaissent pendant un essai et en divisant par la durée de l’essai. Nous dénotons le taux de comptage des pointes par $r$,
| $$\bbox[white,8px] { r= \frac{n}{T} = \frac{1}{T} \int_{O}^{T} d\tau \rho (\tau )} \label{ref4}$$ |
La seconde égalité découle du fait que $\int_{O}^{T} d\tau \rho (\tau ) = n$ et indique que le taux de comptage des pointes est la moyenne temporelle de la fonction de réponse neurale sur la durée de l’essai.
Le taux de comptage des pointes peut être déterminé à partir d’un seul essai, mais au prix de perdre toute résolution temporelle sur les variations de la réponse neurale au cours de l’essai. Un taux de déclenchement dépendant du temps peut être défini en comptant les pics sur de courts intervalles de temps, mais cela ne peut plus être calculé à partir d’un seul essai. Par exemple, nous pouvons définir le taux d’allumage au temps t pendant un essai en comptant tous les pics qui se sont produits entre les temps $t$ et $t + \Delta t$, pour un petit intervalle $\Delta$t, et en divisant ce compte par $\Delta$t. Cependant, pour un petit $\Delta$t, qui permet une résolution temporelle élevée, le résultat du nombre de pointes sur un essai donné est susceptible d’être égal à 0 ou 1, donnant seulement deux valeurs possibles de taux d’allumage. La solution à ce problème consiste à faire la moyenne sur plusieurs essais. Ainsi, nous définissons le taux de tir dépendant du temps comme le nombre moyen de pointes (moyenné sur des essais) apparaissant pendant un court intervalle entre les temps $t$ et $t + \Delta$t, divisé par la durée de l’intervalle.
Le nombre de pointes se produisant entre les temps $t$ et $t + \Delta t$ sur un seul essai est l’intégrale de la fonction de réponse neurale sur cet intervalle de temps. Le nombre moyen de transitoires durant cet intervalle est l’intégrale de la fonction de réponse neuronale moyennée par l’essai. Nous utilisons des parenthèse angulaires,$\langle \rangle $, pour désigner des moyennes sur des essais qui utilisent le même stimulus, de sorte que $\langle z \rangle $ pour toute quantité $z$ est la somme des valeurs de z obtenues à partir de nombreux essais impliquant le même stimulus, divisé par le nombre d’essais. La fonction de réponse neuronale moyennée par l’essai est notée $\rho (t)$, et le taux de déclenchement dépendant du temps est donné par
| $$\bbox[white,8px] { r(t)= \frac{1}{\Delta t} \int_{t}^{t + \Delta t} \langle \rho (\tau ) \rangle d\tau} \label{ref5}$$ |
Nous utilisons la notation $r(t)$ pour cette quantité importante (par opposition à $r$ pour le taux de comptage des pointes), et quand nous utilisons le terme «taux de rendement» sans aucun modificateur, nous entendons $r(t)$. Formellement, la limite $\Delta t$ → 0 devrait être prise du côté droit de cette expression, mais, en extrayant un taux de déclenchement dépendant du temps des données, la valeur de $\Delta t$ doit être assez grande pour qu’il y ait un nombre suffisant de pointes dans le intervalle définissant r(t) pour obtenir une estimation fiable de la moyenne.
Pour des $\Delta t$ suffisament petits, $ r(t) \Delta t$ est le nombre moyen de pointes se produisant entre les temps $t$ et $t + \Delta t$ sur plusieurs essais. Le nombre moyen de pointes sur un intervalle de temps plus long est donné par l’intégrale de r (t) sur cet intervalle. Si $\Delta t$ est petit, il n’y aura jamais plus d’un pic dans l’intervalle entre $t$ et $ t + \Delta t$ T sur un essai donné. Cela signifie que $ r(t) \Delta t$ est aussi la fraction des essais sur lesquels un pic s’est produit entre ces temps.
De manière équivalente, $ r(t) \Delta t$ est la probabilité qu’un pic se produise pendant cet intervalle de temps. Cette interprétation probabiliste fournit une définition formelle du taux d’allumage dépendant du temps; $ r(t) \Delta t$ est la probabilité qu’un pic se produise pendant un court intervalle de temps $\Delta t$ autour du temps t.
Dans toute expression intégrale telle que l’équation ($\ref{ref2}$), la fonction de réponse neurale génère une contribution chaque fois qu’un pic se produit. Si nous utilisons à la place la fonction de réponse à la moyenne des essais, comme dans l’équation ($\ref{ref5}$), cela génère des contributions proportionnelles à la fraction des essais sur laquelle un pic s’est produit.
En raison de la relation entre cette fraction et le taux de tir, nous pouvons remplacer la fonction de réponse neuronale moyennée par l’essai par le taux de tir $r(t)$ dans toute intégrale, par exemple,
| $$\bbox[white,8px] {\int h(\tau ) \langle \rho (t) (t -\tau ) \rangle d\tau = \int h(\tau ) r(t) (t -\tau ) d\tau } \label{ref6}$$ |
pour toute fonction h. Ceci établit une relation importante entre la fonction de réponse neuronale moyenne et le taux de déclenchement; les deux sont équivalentes lorsqu’elles sont utilisées à l’intérieur des intégrales. Ceci fournit également une autre interprétation de $r(t)$ comme étant la densité moyenne des pointes le long de l’axe temporel.
De la même manière que la fonction de réponse $\rho (t)$ peut être moyennée à travers les essais pour donner le taux de tir $r(t)$, le taux de décharge peut être moyenné sur des essais, donnant une quantité que nous appelons le taux moyen de tirs.
Ceci est indiqué par$\langle r \rangle$ et est donné par :
| $$\bbox[white,8px] {\langle r \rangle = \frac{\langle n \rangle}{T}=\frac{1}{T} \int_0^T{ \langle \rho (\tau) \rangle d\tau} =\frac{1}{T} \int_0^T{ r(t) dt }} \label{ref7}$$ |
La première égalité indique que $\langle r \rangle$ est simplementle nombre moyen de pointes par essai divisé par la durée de l’essai. La troisième égalité découle de l’équivalence du taux de tir et de la fonction de réponse neuronale moyenne des essais au sein des intégrales (équation $\ref{ref6}$). Le taux d’allumage moyen est égal à la moyenne temporelle de $r(t)$ et à la moyenne d’essai du taux de comptage des pointes $r$. Bien sûr, un taux de décompte des pointes et un taux de tir moyen peuvent être définis en comptant les pointes sur n’importe quelle période de temps, pas nécessairement toute la durée d’un procès.
Le terme «taux de combustion» est couramment utilisé pour les trois quantités, $r(t)$, r et $\langle r \rangle$. Dans la mesure du possible, nous utilisons respectivement les termes «taux de tir», «taux de comptage» et «taux de tir moyen» pour $r(t)$, $r$ et $\langle r \rangle$, mais lorsque cela devient trop lourd, les différentes notations mathématiques servent à les distinguer. En particulier, nous distinguons le taux de comptage de pointes r du taux de tir $r(t)$ en fonction du temps en utilisant une police différente et en incluant l’argument time dans cette dernière expression (sauf si $r(t)$ est indépendant du temps).
Le taux de tir $r (t)$ ne peut pas être déterminé exactement à partir des données limitées disponibles à partir d’un nombre fini d’essais. De plus, il n’y a pas de façon unique d’approximer $r (t)$. Une discussion des différentes méthodes nous permet d’introduire le concept d’un filtre linéaire et d’un noyau qui sera largement utilisé dans les chapitres suivants. Nous illustrons ces méthodes en extrayant les taux de décharge d’un seul essai, mais des résultats plus précis pourraient être obtenus en faisant la moyenne sur plusieurs essais.
La figure 1.4 compare un certain nombre de façons d’approximer $r (t)$ à partir d’une séquence de pointes. La figure 1.4A montre 3 s de la réponse d’un neurone dans le cortex inféro-temporal enregistré alors qu’un singe regardait une vidéo. Les neurones dans la région du cortex où cet enregistrement a été fait sont sélectifs pour les images visuelles complexes, y compris les visages. Un moyen simple d’extraire une estimation du taux de tir à partir d’un tel train de pointes est de diviser le temps en intervalles distincts de durée? T, de compter le nombre de pics dans chaque case et de diviser par $\Delta t$. La figure 1.4B montre le taux d’allumage approximatif calculé en utilisant cette procédure avec une taille de bac de 100 ms. Notez qu’avec cette procédure, la quantité calculée est en réalité le taux de décharge du nombre de pointes sur la durée du bac, et que le taux de tir r (t) dans un bac donné est approché par ce taux de comptage de pointes.