Les graphes et leurs représentations

Définitions et exemples

De nombreuses situations du monde réel peuvent être commodément décrites au moyen d’un diagramme constitué d’un ensemble de points et de lignes reliant certaines paires de ces points.
Par exemple, les points peuvent représenter des personnes, avec des lignes rejoignant des paires d’amis; ou les points pourraient être des centres de communication, avec des lignes représentant des liens de communication. Notez que dans de tels diagrammes, on s’intéresse principalement à savoir si deux points donnés sont joints par une ligne; la manière dont ils sont joints est immatérielle. Une abstraction mathématique de situations de ce type donne naissance au concept de graphe.
Un graphe G est une paire ordonnée ($V (G)$, $E (G)$) constituée d’un ensemble $V (G)$ de sommets et d’un ensemble $E (G)$, disjoint de $V (G)$, de bords, avec une fonction  incidence $ψ_G$ qui associe à chaque arête de G une paire non ordonnée de sommets (pas nécessairement distincts) de G.
Si e est un arête et u et v sont des sommets tels que $ψ_G (e) = \lbrace u, v\rbrace$, alors e  joint u et v, et les sommets u et v sont appelés les extrémités de e.
On note les nombres de sommets et d’arêtes dans G par $v (G)$ et $e (G)$; ces deux paramètres de base sont appelés l’ordre et la taille de G, respectivement.

Deux exemples de graphiques devraient servir à clarifier la définition. Pour simplifier la notation, nous écrivons $uv$ pour la paire non ordonnée $\lbrace u, v\rbrace$.

• Exemple 1:

$V (G) = \lbrace u,v,w,x,y \rbrace$ et $E(G) = \lbrace a,b,c,d,e,f,g,h\rbrace$

$ψ_G$ est défini par

$ψ_G(a) = uv$
$ψ_G(b) = uu$
$ψ_G(c) = vw$
$ψ_G(d) = wx$
$ψ_G(e) = vx$
$ψ_G(f) = wx$
$ψ_G(g) = ux$
$ψ_G(h) = xy$

• • Exemple 2:

$H = (V (H),E(H))$
où $V (H) = \lbrace v_0,v_1,v_2,v_3,v_4,v_5\rbrace$ et $E(H) = \lbrace e_1,e_2,e_3,e_4,e_5,e_6,e_7,e_8,e_9,e_{10}\rbrace$

$ψ_H$ is defined by

$ψ_H(e_1) = v_1v_2$
$ψ_H(e_2) = v_2v_3$
$ψ_H(e_3) = v_3v_4 $
$ψ_H(e_4) = v_4v_5 $
$ψ_H(e5) = v_5v_1$
$ψ_H(e_6) = v_0v_1$
$ψ_H(e_7) = v_0v_2$
$ψ_H(e_8) = v_0v_3$
$ψ_H(e_9) = v_0v_4 $
$ψ_H(e_{10}) = v_0v_5$

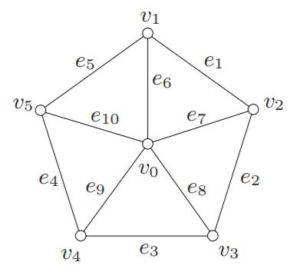
Les graphes sont ainsi nommés parce qu’ils peuvent être représentés graphiquement, et c’est cette représentation graphique qui nous aide à comprendre beaucoup de leurs propriétés. Chaque sommet est indiqué par un point, et chaque bord par une ligne joignant les points représentant ses extrémités. Les diagrammes de G et H sont illustrés sur les figures ci-dessus. (Pour plus de clarté, les sommets sont représentés par de petits cercles.)

Il n’y a pas de moyen unique de tracer un graphique; les positions relatives des points représentant les sommets et les formes des lignes représentant les bords n’ont généralement aucune signification. Dans les figures précédentes, les bords de G sont représentés par des courbes, et ceux de H par des segments de droite. Un diagramme d’un graphique représente simplement la relation d’incidence entre ses sommets et ses arêtes. Cependant, nous dessinons souvent un diagramme d’un graphique et nous nous y référons comme le graphique lui-même; dans le même esprit, nous appelons ses points «sommets» et ses lignes «arêtes».

La plupart des définitions et concepts de la théorie des graphes sont suggérés par cette représentation graphique. Les extrémités d’un bord sont dites incidentes avec le bord, et vice versa.
Deux sommets qui sont incidents avec un bord commun sont adjacents, de même que deux arêtes qui sont incidentes avec un sommet commun, et deux sommets adjacents distincts sont des voisins.

L’ensemble des voisins d’un sommet v dans un graphe G est noté NG (v).
Un bord avec des extrémités identiques est appelé une boucle, et un bord avec des extrémités distinctes un lien.
Deux ou plusieurs liens avec la même paire d’extrémités sont dits parallèles. Dans le dessin du graphe G, le bord b est une boucle, et tous les autres bords sont des liens; les arêtes d et f sont des arêtes parallèles.

Tout au long de cette partie, la lettre G dénote un graphique. De plus, quand il n’y a pas de possibilité d’ambiguïté, on omet la lettre G des symboles de la théorie des graphes et on écrit, par exemple, V et E au lieu de V (G) et E (G).
Dans de tels cas, nous notons les nombres de sommets et les arêtes de G par n et m, respectivement.

Un graphe est fini si ses deux ensembles de sommets et de sommets sont finis.

Dans cette partie, nous étudions principalement les graphes finis, et le terme «graphe» signifie toujours «graphe fini». Le graphique sans sommets (et donc sans bords) est le graphe nul.
Tout graphique avec un seul sommet est appelé trivial. Tous les autres graphiques sont non triviaux.
Nous admettons l’existence d’un graphique nul uniquement pour des raisons de commodité mathématique.

Ainsi, sauf indication contraire, tous les graphiques en discussion doivent être considérés comme non-normaux.
Un graphique est simple s’il n’a pas de boucles ou de bords parallèles.
Le graphe H de l’exemple 2 est simple, alors que le graphe G de l’exemple 1 ne l’est pas.

Une grande partie de la théorie des graphes concerne l’étude de graphes simples.

Un ensemble V, avec un ensemble E de sous-ensembles de deux éléments de V, définit un graphe simple (V, E), où les extrémités d’un bord uv sont précisément les sommets u et v.
En effet, dans n’importe quel graphe simple, on peut se passer de la fonction d’incidence ψ en renommant chaque arête comme la paire non ordonnée de ses extrémités. Dans un diagramme d’un tel graphe, les étiquettes des bords peuvent alors être omises.