Nous commençons par considérer comment modéliser une souris qui se déplace dans un labyrinthe. Le labyrinthe est un espace fermé contenant neuf pièces. L’espace est divisé en trois par trois, avec des portes reliant les pièces, comme le montre la figure ci-dessous
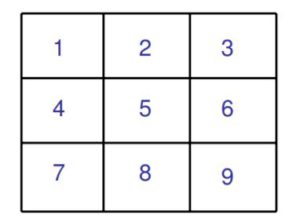
Il y a des portes menant aux pièces adjacentes, verticalement et horizontalement. En particulier, il y a les portes suivantes:
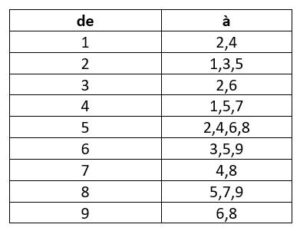
Nous supposons que la souris est une souris de Markov; c’est-à-dire que la souris se déplace de façon aléatoire d’une pièce à l’autre, la distribution de probabilité de la pièce suivante ne dépendant que de la pièce actuelle, et non de l’historique de la pièce actuelle. (Ceci est la propriété de Markov.) De plus, nous supposons que la souris est également susceptible de choisir chacune des portes disponibles dans la pièce qu’elle occupe. (C’est une propriété spéciale au-delà de la propriété Markov.)
Nous allons modélisé le mouvement de la souris comme une chaîne de Markov. L’état de la chaîne de Markov est la pièce occupée par la souris. Nous laissons l’index temporel $n$ se référer à la $n^{ième}$ salle visitée par la souris. Nous créons donc une chaîne de Markov en temps discret.
Plus précisément, nous laissons $X_n$ être l’état (pièce) occupé par la souris au pas (ou à l’heure ou à la transition) $n$. La pièce initiale est $X_0$. La pièce après la première transition est $X_1$, et ainsi de suite.
Ainsi {$X_n$: n ≥ 0} est la chaîne de Markov en temps discret (DTMC); c’est un processus stochastique à états discrets à temps discret. La souris se trouve dans la pièce $X_n$ (une variable aléatoire) après avoir fait $n$ mouvements, après avoir démarré dans la pièce $X_0$, qui pourrait aussi être une variable aléatoire.
Nous allons spécifier l’évolution de la chaîne de Markov en définissant les probabilités de transition via une matrice de transition.
Pour notre exemple, faire un modèle de chaîne de Markov en temps discret consiste à définir une matrice de transition de Markov 9 × 9 cohérente avec la spécification ci-dessus.
Pour la plupart des personnes, spécifier la matrice de transition signifie spécifier le modèle.
Nous devons aussi dire comment nous commençons, le point de départ pourrait être aléatoire, auquel cas la position initiale serait spécifiée par un vecteur de probabilité.
