Le travail de Harry Wiener repose sur une idée fondamentale promulguée par lui pendant les années 1947-1948. Cette idée était que la structure d’une molécule pourrait être utilisée pour dériver des paramètres mathématiques qui pourraient ensuite être utilisés pour caractériser cette molécule dans une variété de contextes différents. En d’autres termes, il a affirmé que les descripteurs mathématiques seraient aussi efficaces que les propriétés physicochimiques déterminées expérimentalement dans la caractérisation des espèces moléculaires. Au fil des ans, cette remarquable perspicacité a été démontrée à maintes reprises, même si les recherches de Wiener étaient très étonnamment limitées à l’étude des alcanes.
Les deux paramètres mathématiques avancés par Wiener sont maintenant généralement désignés comme des invariants topologiques et ils étaient spécifiquement destinés à permettre la distinction entre les isomères structurels de divers membres de la série des alcanes. De nombreuses études effectuées sur des espèces d’hydrocarbures dans la première moitié du XIXe siècle ont établi que la majorité des hydrocarbures pouvaient être classés comme appartenant à certaines séries homologues. Dans une telle série, les membres immédiatement adjacents de la série diffèrent dans leur structure par un seul groupe méthylène, c’est-à-dire par un motif $CH_2$. Kekulé (1858) a été le premier à reconnaître que les alcanes formaient une série homologue et que la série dans son ensemble pouvait être représentée par la formule générale $C_nH_{2n + 2}$ où n est le nombre d’atomes de carbone dans la molécule.
La première analyse graphique des membres de la série des alcanes a été entreprise par le mathématicien Cayley, dont le travail a abouti à une méthode de calcul du nombre d’isomères structuraux associés à chaque membre de la série (Cayley, 1874). Il a montré que, bien que le nombre total d’isomères augmente très lentement pour les premiers membres de la série, le nombre d’isomères se met à augmenter de plus en plus rapidement quand n croit.
Ainsi, les trois premiers membres de la série avec n = 1, 2, 3 ($CH_4$, $C_2H_6$, $C_3H_8$) ont chacun un isomère et le quatrième membre ($C_4H_8$) en a seulement deux.
En revanche, les techniques modernes de dénombrement des isomères computationnels ont établi que le vingtième membre ($C_{20}H_{42}$) a 366 319 isomères structurels alors que ce nombre pour le cinquantième membre ($C_{50}H_{102}$) passe à 1 117 743 651 746 953 270 (Knop et al. 1985).
Des études de ce genre révèlent très clairement que la caractérisation de manière unique de tous les isomères dans les séries homologues devient vraiment impossible pour les valeurs supérieure à 12. En fait, chaque fois que n dépasse douze, de sérieux problèmes commencent à se poser.
Les deux méthodes de caractérisation des espèces moléculaires couramment utilisées aujourd’hui ont évolué à partir de travaux beaucoup plus anciens menés il y a plus de 150 ans. Nos méthodes contemporaines de résolution du problème reposent
- soit sur la mesure expérimentale de certaines propriétés moléculaires appropriées,
- soit sur le calcul théorique de certains paramètres moléculaires considérés comme caractérisant l’espèce en question.
La première approche bien qu’étant certainement utile dans certains cas est vouée à l’échec parce que l’objectif ici est de prédire le comportement moléculaire plutôt que de le mesurer.
La deuxième approche, qui découle d’études approfondies sur les espèces d’hydrocarbures menées par Kopp dans les années 1840 (Kopp, 1842a, Kopp, 1842b), est celle que nous présenterons dans ce chapitre. L’étude détaillée de Kopp sur les variations du point d’ébullition pour les membres de plusieurs séries homologues l’a amené à formuler des relations algébriques entre les membres qui ont été exprimées sous forme d’ensembles d’équations.
Ce travail est maintenant largement considéré comme la première formulation du principe dit d’additivité qui affirme que toute propriété d’une substance chimique peut être déterminée simplement en additionnant les contributions à cette propriété de chacun des atomes des molécules constituant la substance (Rouvray, 1991).
Pour mettre pleinement en scène la percée pionnière de Wiener, il faut d’abord examiner de plus près le rôle joué par le principe d’additivité.
Au fil des années, le principe d’additivité a été appliqué dans de nombreux contextes différents et a été utilisé pour faire des prédictions pour une vaste gamme de systèmes différents. Ses prédictions ont été examinées de près, ce qui a permis de conclure que le principe de l’additivité ne peut généralement pas être utilisé pour obtenir des résultats satisfaisants. Bien que, dans certains cas précis que nous citons ci-dessous, le principe puisse prétendre à des antécédents raisonnables, il a été démontré dans la majorité des cas qu’il était invalide (Zahn, 1934, Taylor et al., 1945, Somayajulu et al. 1965).
En conséquence, il est justifié de conclure qu’aucune propriété moléculaire ne peut être considérée comme strictement additive. Par exemple, il convient de mentionner que cette affirmation est vraie même pour la propriété moléculaire qui se rapproche le plus de l’additivité, à savoir la masse moléculaire, qui est presque exactement la somme des masses atomiques pertinentes.
La seule validité que le principe d’additivité n’ait jamais eu était une approximation et même alors son domaine d’application était plus ou moins limité aux membres des séries homologues et des espèces congénériques. La raison sous-jacente de ceci est que dans de telles molécules, il existe habituellement une transférabilité approximative des forces interatomiques et des liaisons chimiques du même type d’une molécule à l’autre (Altona et Faber, 1974). Cette applicabilité limitée, cependant, est à peine suffisante pour qualifier le principe d’additivité en tant qu’outil efficace et polyvalent. L’avènement d’un tel outil a dû attendre les contributions séminales de Wiener dans ce domaine.
Levée de rideaux
Les contributions de Wiener à la chimie ont été faites au cours des années 1947-1948 et ont pris la forme de cinq articles publiés dans les principaux journaux de chimie américains de cette époque (Wiener, 1947a, 1947b, 1947c, 1948a, 1948b). Collectivement, ces publications se sont avérées très significatives pour diverses raisons que nous allons maintenant explorer.
Peut-être avant tout, le travail de Wiener a constitué une percée en ce sens qu’il a présenté pour la première fois une nouvelle façon de prédire le comportement et les propriétés des espèces moléculaires. Jusqu’à l’avènement des idées novatrices de Wiener, cela ne pouvait être tenté qu’en utilisant le principe d’additivité souvent inefficace et faillible. En effet, un paramètre qui était couramment utilisé à des fins prédictives avant le travail de Wiener était l’indice de nombre de carbone, n, qui était dérivé simplement en additionnant le nombre d’atomes de carbone contenus dans certaines espèces d’hydrocarbures.
Bien que ce paramètre ait été utilisé pendant de nombreuses décennies avant l’arrivée de Wiener sur la scène, il avait été généralement reconnu comme extrêmement limité dans les prédictions qu’il était capable de faire. Un certain nombre des premières applications de ce paramètre ont été discutées par Rouvray (1991).
L’approche de Wiener représente une rupture majeure avec la notion simple d’additivité et ouvre la voie à une manière beaucoup plus sophistiquée de caractériser les espèces moléculaires. Les paramètres de la théorie graphique de Wiener pourraient être interprétés comme modélisant des caractéristiques de molécules telles que la surface, la forme et la distribution de charge.
Les deux paramètres introduits par Wiener ont été exposés dans le premier de ses cinq articles (Wiener 1947a). Ces paramètres ont été conçus dans le but spécifique de corréler les points d’ébullition des membres de la série des alcanes avec leur structure moléculaire.
- Le premier des paramètres qu’il a désigné est l’indice de polarité, p, qui est défini comme « le nombre de paires d’atomes de carbone qui sont séparés par trois liaisons carbone-carbone ».
- Le second des paramètres de Wiener a été décrit comme l’indice de Wiener, w, et est défini comme « la somme des distances entre deux atomes de carbone dans la molécule, en termes de liaisons carbone-carbone ».
Voici l’exemple du calcul des indices de polarité et de Wiener dans le cas de la molécule 3-méthylpentane:
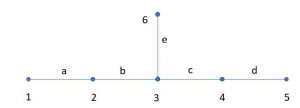
L’indice de polarité est égal à 4. En effet, on trouve les couples (1,6), (2,4), (1,5) et (2,6)
Pour obtenir l’indice de Wiener, il faut multiplier le nombre d’atomes de carbone d’un côté de n’importe quelle liaison par ceux de l’autre côté;
Le nombre de liaisons est égal à 5 :
- (1,2) liaision a
- (2,3) liaision b
- (3,4) liaision c
- (4,5) liaision d
- (3,6) liaision e
| Liaison a | $1×5$ | (1) | (2)(3)(4)(5)(6) |
| Liaison b | $2×4$ | (1)(2) | (3)(4)(5)(6) |
| Liaison c | $2×4$ | (4)(5) | ((1)(2)(3)(6) |
| Liaison d | $1×5$ | (5) | (1)(2)(3)(6)(4) |
| Liaison e | $1×5$ | (5) | (4)(3)(6)(2)(1) |
w est la somme de ces valeurs de la colonne 2 pour toutes les liaisons.
($1×5$), ($2×4$),($2×4$),($1×5$),($1×5$)
Lorsque les espèces alcanes existent sous la forme de chaînes linéaires, le calcul des deux paramètres est facilité. Il peut être dérivé des expressions analytiques que Wiener a données pour les alcanes normaux, à savoir
| $$\bbox[white,8px]{ p=n-3}$$ |
| $$\bbox[white,8px]{w=\frac{1}{6}(n-1)n(n+1) = \frac{(n^3 -n)}{6}}$$ |
où n est le nombre d’atomes dans la molécule.
À ce sujet, nous mentionnerons également que plusieurs autres expressions analytiques de ce type ont depuis été publiées par divers auteurs. Ainsi, en 1976, Entringer et ses collaborateurs ont établi que pour les graphes cycliques avec un nombre pair de sommets, l’expression prend forme:
| $$\bbox[white,8px]{w=\frac{n^3}{8}}$$ |
alors que pour de tels graphes avec un nombre impair de sommets, l’expression devient:
| $$\bbox[white,8px]{w=\frac{n^3-n}{8}}$$ |
Bonchev et Trinajstic. (1977) ont dérivé des expressions pour une variété de graphes arborescents et ont pu montrer, par exemple, que le graphe en étoile avait un indice de Wiener de la forme générale:
| $$\bbox[white,8px]{w=(n-1)^2}$$ |
Une procédure récursive pour le calcul de w pour tout type d’arbre, quelle que soit la quantité de ramification, a été mise en avant par Canfield et af. (1985). Pour une discussion beaucoup plus détaillée de ce thème, le lecteur peut lire Rouvray (1986).
La motivation de Wiener, en mettant en avant ses deux paramètres, était de trouver un moyen de composer avec la ramification présente dans les isomères de la série des alcanes. Il est à noter qu’en développant ses paramètres, Wiener n’a porté aucune attention aux atomes d’hydrogène dans les espèces d’alcanes qu’il a étudiées. Il y avait une bonne raison à cela, à savoir que les atomes d’hydrogène ne sont nullement déterminants sur la structure.
Les structures adoptées par les espèces d’alcanes, ainsi que celles trouvées dans la plupart des membres d’autres séries homologues, sont formées par la liaison covalente $\sigma$ qui maintient l’ensemble de la charpente des liaisons carbone.
Une fois ce cadre en place, les atomes d’hydrogène sont ajoutés pour satisfaire la tétravalence des atomes de carbone. Ceux-ci ont une influence relativement faible par rapport à la densité d’électrons entourant chaque atome de carbone et ne modifient certainement pas la structure du carbone sous-jacente.
Ainsi, Wiener ignora à juste titre les atomes d’hydrogène, en se concentrant uniquement sur les atomes de carbone.
Cette approche est encore très utilisée aujourd’hui. Lorsque l’indice de Wiener ou d’autres paramètres sont calculés pour des espèces moléculaires, les atomes d’hydrogène sont négligés dans pratiquement tous les cas. Les graphiques utilisés pour calculer ces paramètres sont décrits comme des graphiques à suppression d’hydrogène. Wiener fut donc aussi un pionnier en reconnaissant que les atomes d’hydrogène n’avaient qu’un rôle mineur à jouer dans la détermination des propriétés des membres des séries homologues. Nous allons décrire maintenant la manière quelque peu inhabituelle avec laquelle Wiener utilisa ses paramètres.
Wiener a commencé en appliquant ses deux paramètres à la prédiction des points d’ébullition de divers membres de la série des alcanes. Cependant, ni dans cette première application, ni dans aucune de ses études ultérieures, il n’a utilisé directement ses paramètres pour caractériser les espèces, ce qui serait fait normalement de nos jours. Au lieu de cela, Wiener basa son approche sur une méthode de différence qui impliquait d’abord de déterminer le paramètre pour une molécule de référence, puis de soustraire de celle-ci la valeur du paramètre pour la molécule spécifique à caractériser. Le processus peut s’exprimer comme suit:
| $$\bbox[white,8px]{\Delta P = P_{spec}-P_{ref} }$$ |
La molécule de référence a dans tous les cas été choisie pour être une espèce à chaîne droite, c’est-à-dire une molécule d’alcanes sans branchement. Cela signifiait que les valeurs $\Delta w$ obtenues étaient soit nulles (dans le cas des alcanes normaux), soit positives puisque les valeurs w pour les espèces ramifiées sont toujours plus petites que pour les chaînes non ramifiées. D’autre part, les valeurs de $\Delta p$ supposaient des valeurs nulles, positives ou négatives, bien que pour toutes les espèces avec n $\geqslant 6$, les valeurs n’étaient que négatives ou nulles.
Wiener supposa que les points d’ébullition des alcanes répondraient à une formule linéaire du type:
| $$\bbox[white,8px]{t_b = aw + bp + c \\ \text{ où } t_b \text{ est le point d’ébullition d’un alcane donné, a, b et c sont des constantes, et w et p sont les paramètres structuraux de Wiener discutés plus tôt}} \label{tb}$$ |
Pour continuer sur sa lancée, toutefois, Wiener avait besoin de différences dans son équation plutôt que de valeurs absolues pour les termes $t_b$, w et p. L’équation requise a été facilement obtenue en soustrayant de l’équation ($\ref{tb}$) une équation du même type général pour obtenir une équation de la forme:
| $$\bbox[white,8px]{ \Delta t = a\Delta w + b \Delta p }\label{tbdelta}$$ |
où $\Delta t$ représente maintenant la différence des points d’ébullition pour une molécule d’alcane normale et une autre molécule d’alcane contenant le même nombre d’atomes de carbone, $\Delta w$ est la différence correspondante de leur indice de Wiener, et $\Delta p$ la différence correspondante de leurs indices de polarité. De plus, Wiener a pu établir (Wiener, 1947a) que la constante a pourrait être exprimée comme:
| $$\bbox[white,8px]{ a =\frac{k}{n^2} \text{ où k est une nouvelle constante.} }\label{atbdelta}$$ |
Wiener détermina les constantes k et b en utilisant des données de point d’ébullition connues pour 37 espèces d’alcanes différentes (allant des butanes jusqu’aux octanes) afin d’appliquer la corrélation exprimée via l’équation ($\ref{tbdelta}$). L’équation de corrélation qu’il obtint à partir d’une procédure d’ajustement des moindres carrés avait la forme suivante:
| $$\bbox[white,8px]{ \Delta t = \frac{98}{n^2} \Delta w + 5.5 \Delta p }\label{tbdeltacorre}$$ |
et l’écart moyen du point d’ébullition était de $0,47$ °C.
Wiener utilisa ensuite son équation ($\ref{tbdeltacorre}$) pour calculer les points d’ébullition de 29 espèces de nonanes et de 28 espèces de décanes pour lesquelles des points d’ébullition expérimentaux raisonnablement précis étaient déjà connus. Il a pu démontrer que sa méthode donnait les points d’ébullition des 29 nonanes avec un écart moyen de $1,26$°C et les points d’ébullition des 28 décanes avec un écart moyen de $1,30$°C. Le résultat global très satisfaisant que Wiener obtint était donc un écart de seulement $0,97$°C pour un total de 94 espèces d’alcanes.
Ce résultat étonnamment bon encouragea Wiener à entreprendre un certain nombre de corrélations supplémentaires basées sur des équations ayant la même forme générale que l’équation ($\ref{tbdelta}$).
Il est intéressant de noter que dans son premier article, Wiener ne fait aucune prédiction pour les propriétés des alcanes qui n’ont pas encore été déterminées expérimentalement et publiées dans des tableaux produits par l’American Petroleum Institute (1944-1946).
Mis en confiance par les succès de son approche, Wiener se permit de faire des prédictions de diverses propriétés n’ayant pas encore été mesurées. Par exemple, dans son second article (Wiener, 1947b), il utilisa les données connues des tables de l’American Petroleum Institute (1944-1946) sur les chaleurs de combustion, de formation et de vaporisation de 33 alcanes (allant des pentanes aux octanes) et obtint les deux équations suivantes:
| $$\bbox[white,8px]{ -\Delta H_{iso} = \frac{15.5}{n^2} \Delta w + 1.1 \Delta p }\label{hdeltacorre}$$ |
où $\Delta H_{iso}$ est la chaleur d’isomérisation de la réaction :
$$ normal – C_nH_{2n+2} \rightarrow iso – C_nH_{2n+2}$$
à la pression de saturation et à 25°C.
| $$\bbox[white,8px]{ \Delta H_{normal}^{vap} -\Delta H_{iso}^{vap} = \frac{0.412}{n-3} \Delta w + 0.22 \Delta p }\label{vapdeltacorre}$$ |
les termes $\Delta H_{normal}^{vap}$ et $\Delta H_{iso}^{vap}$ représentant respectivement les chaleurs de vaporisation pour les formes normales (n) et pour les isomères des alcanes corrélés.
En utilisant les équations ($\ref{hdeltacorre}$) et ($\ref{vapdeltacorre}$), Wienner les utilisa pour prédire les chaleurs d’isomérisation et de vaporisation de 35 nonanes.
De même, dans son quatrième article, Wiener (1948a) présente les valeurs calculées des constantes A, B et C dans l’équation d’Antoine:
| $$\bbox[white,8px]{ t = \frac{B}{A – log(P)} -C }\label{antoine}$$ |
où t est le point d’ébullition à la pression P.
Après avoir montré que les différences $\Delta A$ et $\Delta B$ peuvent être exprimées sous la forme
| $$\bbox[white,8px]{ \Delta A =\frac{0.45}{n^2} \Delta w + 0.022 \Delta p }\label{deltaA}$$ |
| $$\bbox[white,8px]{ \Delta B =\frac{400}{n^2} \Delta w + 27 \Delta p }\label{deltaB}$$ |
Wiener continua à calculer les valeurs alors inconnues de A, B et C pour chacun des
34 nonanes ramifiés. Dans le cinquième article de Wiener (1948b), des relations furent établies pour prédire la tension superficielle, la dispersion spécifique et la température critique de la solution pour l’ensemble des 35 nonanes.
La dispersion spécifique, $\sigma$, fut définie comme suit:
| $$\bbox[white,8px]{\sigma =\frac{(\mu_d – \mu_c)\times 10^4}{\delta}}$$ |
où $\mu_d$ et $\mu_c$ sont les indices de réfraction respectifs du sodium et d’hydrogène et $\delta$ la densité de la molécule.
Extension de l’approche
Altenburg (1962-1966) présenta le concept d’un rayon carré moyen applicable aux molécules d’alcane. Ce rayon a été défini pour un modèle tridimensionnel flexible réputé refléter le comportement des alcanes. Le modèle consistait en un ensemble de points de masse situés dans l’espace aux positions occupées par chacun des atomes de carbone dans la molécule d’alcane. La rotation libre était autorisée sur tous les axes carbone-carbone (liaison) à condition qu’aucun des angles de liaison ne soit déformé.
La moyenne des rayons au carré , $\overline{R^2}$ , pour un tel modèle peut être exprimé comme:
| $$\bbox[white,8px]{\overline{R^2} =\frac{1}{n} \sum_{i=1}^n {r_i^2}}$$ |
où n est le nombre de points de masse (atomes de carbone) et les termes $r_i$ représentant la distance du $i^{ème}$ point de masse (atome) au centre de gravité de l’ensemble de points de masse (molécule d’alcane). Il montra que les valeurs de $\overline{R^2}$ « augmentent avec la taille moléculaire, allant de 1,1048 pour le pentane normal à 2,6888 pour le décane normal. Altenburg montra que ces valeurs sont directement proportionnelles aux nombres de chemins de Wiener. Dans son article de 1966, Altenburg compara toutes les méthodes biparamétriques alors connues pour prédire les points d’ébullition des alcanes.
Il conclua qu’en termes d’erreur moyenne dans les valeurs prédites, la méthode de Wiener est l’une des meilleures.
Pourquoi un tel succès ?
Dans ce paragraphe, nous passons brièvement en revue les principales explications avancées à ce jour pour expliquer la haute qualité des corrélations obtenues en utilisant la méthode de Wiener comme outil prédictif. La première tentative a été faite par Wiener lui-même dans son premier article (Wiener, 1947a). Le numéro de chemin, w donne une mesure de la compacité d’une molécule, car plus la distance totale entre toutes les paires d’atomes de carbone est petite, plus la compacité moléculaire sera grande. Une relation inverse est donc impliquée entre le point d’ébullition et la compacité moléculaire en raison du fait que plus une molécule sera compacte, moins le nombre de collisions moléculaires sera important, . En conséquence, une espèce plus compacte consommera moins de chaleur pour compenser les pertes d’énergie résultant des collisions moléculaires et ainsi la température d’ébullition sera plus basse.
Le nombre de polarité a été interprété par Wiener comme une mesure semi-quantitative des forces d’attraction intramoléculaires transmises à travers la chaîne carbonée des atomes. Il a soutenu que, si des atomes de carbone alternatifs dans la chaîne présentent des polarités opposées, alors la force d’attraction inductive totale, F, serait donnée par une expression de la forme:
| $$\bbox[white,8px]{F =k_1 p_1 + k_3 p_3 + k_5 p_5 + …}$$ |
où $p_x$ représente le nombre x des liaisons C_C et $k_x$, les coefficients numériques correspondants. Comme pour toutes les molécules d’alcane contenant n atomes, $p_1$ prend la valeur $n-1$, en première approximation la différence des forces pour deux isomères sera donnée simplement par $k_3 \Delta p_3$. Cette expression est identique à celle utilisée dans l’équation ($\ref{tbdeltacorre}$) si k3 prend la valeur 5.5.
Platt en 1952 a soutenu que le nombre de chemin, w, augmente à peu près comme $n^3$ pour des molécules relativement grandes. La racine cubique de ce nombre, c’est-à-dire $\sqrt[3]{w}$, représente le diamètre moyen pour la molécule en question ou une distance moyenne approximative entre les atomes de carbone dans la molécule. Ceci fournit une mesure inverse grossière de la probabilité qu’une partie de la molécule soit attirée par une autre partie par les forces de van der Waals.
Comme la surface de contact totale possible est approximativement constante dans les isomères, la somme des zones d’auto-contact et de contact externe est également constante. Par conséquent, le numéro de chemin doit permettre une mesure directe de la surface de contact externe de la molécule.
L’interprétation de Platt du rôle joué par p différait de celle de Wiener. Platt a vu en p un indice d’encombrement stérique qui caractérise l’interférence stérique des groupes attachés à des atomes de carbone à trois liens séparés lorsque les liaisons carbone-carbone simples tournent. L’effet de l’encombrement stérique est de rendre moins probable certains des auto-contacts et donc de diminuer la surface de contact intramoléculaire et d’augmenter la surface de contact intermoléculaire. Cependant, parce que les interactions stériques peuvent générer des irrégularités de surface moléculaire, la perte de zones d’auto-contact ne doit pas être compensée par un gain dans les zones de contact externe. L’effet net de l’encombrement stérique est donc de réduire efficacement le volume interne des molécules.
Comme nous l’avons noté plus haut, depuis le travail de Platt (1952), peu d’attention a été accordée à la signification du nombre de polarité. On a généralement supposé que l’interprétation de Platt était correcte et qu’il y avait peu à ajouter à son commentaire (Balaban, 1979).
Dans les années 1980, cependant, le groupe Hosoya commenca à remettre en question toute la base du raisonnement de Platt (Narumi et Hosoya, 1985, Gao et Hosoya, 1988; voir aussi le chapitre 3 de cette monographie). Des corrélations étendues réalisées par ces chercheurs ont démontré que le nombre de polarité était un paramètre hautement approprié pour caractériser les propriétés globales des alcanes, telles que la densité à l’état liquide, l’indice de réfraction et le volume moléculaire.
Le fait que le nombre de polarité produise des corrélations beaucoup plus faibles avec la plupart des autres types de propriétés des alcanes a conduit le groupe Hosoya à affirmer que ce nombre était en fait une mesure de l’encombrement d’une molécule. Ils ont affirmé, en outre, que le nombre de polarité ne permet pas de caractériser les facteurs d’encombrement stérique fonctionnant dans les molécules d’alcane comme Platt l’avait maintenu. À l’heure actuelle, on ne peut pas dire que l’affaire soit résolue, bien qu’il semble que les arguments avancés par le groupe Hosoya aient plus de chances d’être justifiés à long terme.
L’interprétation de la signification physique de l’indice de Wiener, w, a prouvé être encore plus controversé que celui du nombre de polarité, p. La première tentative de résolution de cette question au moyen d’une corrélation appropriée a été entreprise par Motoc et Balaban (1981). Ces chercheurs ont démontré que le nombre de trajets reproduit fidèlement le volume de van der Waals des molécules d’alcanes. Pour divers alcanes en C4-C8, ils ont obtenu un coefficient de corrélation supérieur à 0,99. Le volume de van der Waals a été largement utilisé comme limite approximative pour l’extension du nuage d’électrons entourant une molécule, on suppose généralement que la densité électronique tombe effectivement à zéro en dehors de cette limite (Williams et Yau, 1987). D’autres chercheurs ont exprimé leur conviction sur le fait que w reflétait la forme des alcanes, c’est-à-dire qu’ils fournissaient une mesure approximative de la quantité de ramification présente (Wiener, 1947, Bonchev et Trinajstif, 1977). Bien qu’il soit généralement connu que w diminue avec l’augmentation de la ramification, une relation précise n’a pu être déterminée car il n’y a pas de mesure absolue de ramification. De plus, une telle relation doit être un peu ténue au mieux. En effet, Rouvray (1988) établit que les points d’ébullition des 75 décanes ne montrent aucune corrélation avec w.
Dans une tentative relativement récente d’expliquer la signification physique de l’indice de Wiener, Gutman et al. (1993) ont conjecturé que ce paramètre représentait le rapport de la surface au volume des molécules d’alcane. Cependant, il ne fallut pas longtemps avant que cette conjecture ne soit abandonnée par Gutman (Gutman et KortvClyesi, 1995). La conclusion supposée définitive de Gutman et Kiirtvdlyesi fut que w représente une mesure de la surface S de l’alcane. La relation mathématique qu’ils ont obtenue a pris la forme générale:
| $$\bbox[white,8px]{S = \alpha [w]^{\beta} + \gamma }\label{Gutman}$$ |
où $\alpha$, $\beta$, et $\gamma$ sont des constantes à déterminer. On a trouvé que l’équation ($\ref{Gutman}$) donnait les meilleurs coefficients de corrélation lorsque l’exposant $\beta$ prenait des valeurs comprises entre 0,38 et 0,42. Cependant, il semble hautement improbable que ce soit la fin de l’histoire car il est impossible d’interpréter physiquement cette formulation.
L’introduction des matrices
Nous parlons ici de la matrice de distance et de la relation intime qui existe entre cette matrice et l’indice de Wiener. Cette matrice a d’abord été mise en évidence par Hosoya (1971). Elle est habituellement dénotée comme D(G) et représentée comme un tableau réel, carré et symétrique d’ordre q. Ses entrées, désignées par le symbole $d_{ij}$ représentent la distance parcourue en se déplaçant du sommet i au sommet j du graphe G. Dans le présent contexte, toutes ces distances sont en fait le nombre d’arêtes de graphe traversées. Ces distances $d_{ij}$ doivent toujours satisfaire aux trois critères suivants:
1. La relation identité $d_{ii}=0$
2. la relation de symétrie $d_{ij} = d_{ji}$
3. L’inégalité triangulaire $ d_{ij} \leqslant d_{ik} + d_{kj}$
où les indices i, j et k sont compris entre les valeurs 1 2, … q. Les entrées $d_{ij}$ sont définies de manière unique, seulement dans le cas de graphes arborescents. Pour tenir compte des graphes cycliques si souvent rencontrés en chimie, Hosoya (1971) a proposé que $d_{ij}$ soit défini comme le nombre minimum d’arêtes qui doivent être parcourues en passant du sommet i au sommet j du graphe G. Une description détaillée de la matrice de distance et ses nombreuses applications se trouvent dans l’étude de Rouvray (1986).
Nous sommes maintenant en mesure d’élaborer le rôle clé joué par Hosoya dans le développement des idées de Wiener (Hosoya, 1971). Dans cet article de 1971, Hosoya a introduit un nouveau descripteur théorique pour les molécules d’alcanes qu’il a décrit comme étant un indice topologique. Cet index, Z a été défini de la façon suivante:
| $$\bbox[white,8px]{Z = \sum_{k=1}^m p(G,k) }\label{Hosoya}$$ |
où p(G, k) est le nombre de façons dont k déconnecté K, les graphes peuvent être intégrés dans le graphe G et m est la valeur maximale prise par l’entier k. Nous ne discuterons pas de cet indice ici; il a été examiné ailleurs (Hosoya, 1986).
Vers la fin de son article de 1971, Hosoya a souligné que le nombre de chemin, w, est égal à la moitié de la somme des entrées hors diagonales dans la matrice de distance, D(G), pour tout graphique représentant le molécule d’alcane. Ceci implique que les nombres de chemin et de polarité de Wiener peuvent être exprimés en termes d’entrées de matrice de distance comme suit: