Applications de descripteurs moléculaires flexibles dans l’étude QSPR-QSAR des formules hétérocycliques
Référence : Applications of Flexible Molecular Descriptors in the QSPR–QSAR Study of Heterocyclic Drugs (Pablo R. Duchowicz, Eduardo A. Castro, Andrey A. Toropov, Emilio Benfenati)
La connaissance est multifonctionnelle. L’une des applications les plus importantes de la connaissance est de produire de nouvelles connaissances. Malgré l’existence de grandes bases de données sur les structures moléculaires et la croissance continue des données expérimentales numériques sur les propriétés physicochimiques et les activités biologiques, le problème de l’estimation des propriétés des substances non encore testées pourrait se poser de manière plus précise. moins dans les prochaines décennies. Au cours du dernier demi-siècle, il est devenu courant d’utiliser des caractéristiques numériques topologiques, physiques, chimiques et biologiques, pour prédire les propriétés de substances inconnues pour différentes raisons, notamment parce qu’elles sont instables, toxiques ou simplement que leur mesure nécessite trop de temps. Le domaine des sciences naturelles, qui vise à construire des modèles mathématiques pour rechercher des régularités dans les données et permettre leur systématisation, a été traité par la théorie quantitative des relations structure-propriété / activité (QSPR-QSAR).
Il existe plusieurs raisons d’établir et de développer des études QSPR-QSAR. En termes d’aspects économiques, la conception des modèles QSPR-QSAR donne une chance pour l’utilisation rationnelle des ressources disponibles présentes dans le laboratoire ou même un centre de fabrication, et évite d’effectuer des déterminations expérimentales coûteuses et inutiles.
En ce qui concerne les aspects moraux, les modèles QSPR-QSAR appliqués à la toxicologie ont une grande importance dans le criblage virtuel du potentiel toxique des composés avant leur synthèse, et représentent donc une alternative efficace qui réduit les tests sur les animaux dans les essais biologiques.
Enfin, du point de vue théorique, le modèle peut éclairer les mécanismes des propriétés physico-chimiques ou des activités biologiques des composés.
Bien que des études pionnières dans la théorie QSPR-QSAR aient été établies par Wiener en 1947 [1-4], d’autres modèles mathématiques avaient été rapportés précédemment pour la prédiction des propriétés des substances.
Par exemple, il est bien connu que des schémas d’additivité simples et des méthodes de contribution de groupe ont été utilisés avant les premières analyses QSPR-QSAR [5-7].
Nous allons commençer par résumer ces approches.
Le schéma additif simple
L’essence de cette technique pour modéliser une propriété étudiée (P) repose sur l’exécution de sommes de paramètres ($C_k$) associées à une collection de groupes atomiques définis ou de fragments présents dans la molécule, uniquement au moyen d’une compréhension classique:
| $$\bbox[white,8px]{P = \sum_{k=1} C_k }\label{additivity}$$ |
En général, P représente les capacités thermiques [5], les énergies libres de Gibbs [5], les entropies [6], les propriétés thermodynamiques [7] ou technologiques [8] des polymères, et d’autres types de propriétés physicochimiques [9, 10]. Bien qu’il ait été rapporté que le schéma d’additivité simple donne des prédictions raisonnables pour les propriétés d’intérêt [5-8], des prédictions insatisfaisantes ont également été mentionnées dans la littérature [9, 10]. L’un des principaux inconvénients de l’approche additive est l’impossibilité de fournir tous les fragments moléculaires possibles pour tous les produits chimiques disponibles.
Bicerano [8] a cependant décrit un outil pour modéliser les propriétés des polymères en utilisant des indices de connectivité topologique moléculaire (qui peuvent être définis pour n’importe quelle structure), au lieu d’une collection de fragments déterminée au préalable. En fait, la version présentée du schéma additif simple est universelle, et l’approche peut être utilisée avec succès pour prédire les propriétés de n’importe quel type de molécule (pas seulement les polymères) [11, 12]. Il est également intéressant de noter que le schéma additif simple a été utilisé dans la recherche psychonomique [13].
Méthodes de contribution des groupes
La technique de contribution de groupe utilise un type particulier de fonction mathématique pour chaque propriété analysée [14-20], dont les paramètres sont calculés avec les contributions de fragments définis dans la molécule. Le choix des fonctions est fait sur la base de la signification physique et / ou des pratiques antérieures. Par exemple, Iwai et al. [14] ont établi un modèle pour la pression de vapeur des isomères d’alcanes en recourant à la formule suivante :
| $$\bbox[white,8px]{Ln(P_vM) = \left\lbrack \sum_{i=1} n_i(a_i + b_i)/T^* -c_i Ln(T^*) – d_i T^* \right\rbrack + Q}\label{group}$$ |
où $P_v$ est la pression de vapeur saturée, $T^* = T[K]/100$, M est le poids moléculaire, $n_i$ est le compte du $i_{ième}$ groupe dans la structure, Q est un facteur de correction spécifique pour chaque composé, et $a_i$ , $b_i$, $c_i$ et $d_i$ correspondent aux contributions du $i_{ième}$ groupe.
Le premier ensemble de paramètres à utiliser dans l’équation ($\ref{group}$) sont CH4, -CH3, >CH2, >CH- et >C<;
un second ordre de groupes est utilisé pour la définition de Q dans l’équation ($\ref{group}$): – CH(CH3)CH3, CH(CH3)CH2CH3, etc.
Les valeurs numériques pour $a_i$ , $b_i$, $c_i$ et $d_i$ sont choisies de manière à produire les plus petites différences possibles entre les pressions de vapeur expérimentales et prédites.
La méthode de contribution de groupe est largement utilisée dans la recherche biochimique [16, 21].
Descripteurs et leurs applications
Selon Balaban [22] on peut classer les indices topologiques comme appartenant aux classes suivantes:
- Première génération, basée sur des entiers
- Deuxième génération, basée sur des nombres réels
- Troisième génération, basée sur des matrices
- Quatrième génération, qui comprend les caractéristiques stéréochimiques des molécules
- Une autre classe devrait être ajoutée à cette classification: celle basée sur l’optimisation numérique
Le pool de descripteurs moléculaires a considérablement augmenté au cours des dernières décennies, et le problème de la sélection de descripteurs moléculaires optimaux est un sujet d’actualité pour de nombreux chercheurs [23].
Deux procédures principales sont disponibles pour choisir les variables optimales dans les études QSPR-QSAR:
- l’une d’elles consiste à évaluer des milliers de descripteurs moléculaires pour trouver les meilleurs;
- l’alternative repose sur la sélection de quelques descripteurs ajustables et l’optimisation de leurs parties variables, afin de les rendre spécifiques à la propriété-activité étudiée.
La plupart des descripteurs moléculaires disponibles dans la littérature sont de type rigide, c’est-à-dire caractérisés par des valeurs numériques fixes indépendantes de la propriété considérée.
Par conséquent, ces descripteurs peuvent être calculés une fois que le modèle de liaison et la géométrie dans le cas des indices structurels 3D d’une molécule sont connus.
Comme la sélection d’un ensemble de descripteurs réduit optimal parmi des milliers d’entre eux n’est pas une tâche triviale, il faut faire face aux ambiguïtés découlant de la forte corrélation entre les variables.
En revanche, un descripteur flexible ne présente pas ce type de problème et peut conduire à un modèle plus simple, tant du point de vue de la compréhension que du point de vue statistique. Si nous étendons le concept de descripteur moléculaire comme une fonction «variable» ou «flexible» en fonction de certaines parties variables, nous pouvons les optimiser pour chaque propriété considérée lors de l’analyse de régression.
Les études QSPR-QSAR ont traditionnellement été développées en sélectionnant a priori un modèle analytique (typiquement linéaire, polynomial ou log-linéaire) pour quantifier la corrélation entre les indices moléculaires sélectionnés et la propriété d’intérêt, suivi d’une analyse de régression pour déterminer les paramètres de modèle. Bien que les approches ci-dessus se soient révélées utiles dans certains cas, elles présentent un certain nombre de limites. En effet, les relations quantitatives entre la structure moléculaire et les propriétés physicochimiques et biologiques peuvent être plutôt complexes et hautement non linéaires, de sorte que la détermination de la forme analytique optimale du modèle QSPR-QSAR constitue un véritable défi.
De plus, l’analyse de régression devient complexe et moins fiable à mesure que le nombre de descripteurs augmente.
Dans la présente section, nous allons discuter de plusieurs exemples d’études impliquant chaque type d’optimisations mentionnées ci-dessus.
L’indice de connectivité variable des vertex
L’un des indices topologiques les plus adéquats, l’indice de connectivité vertex de premier ordre ($^1\chi$), a été proposé par Milan Randic en 1975 selon la définition suivante [26]:
| $$\bbox[white,8px]{^1\chi = 1/2 \left(\sum_{i,j} deg_i \times deg_j \right)^{-0.5} }\label{randic1}$$ |
où $deg_i$ représente le degré de sommet $v_i$ (le nombre de voisins de $v_i$). La somme s’exécute sur tous les produits possibles de degrés de sommet pour les points de terminaison. Il est à noter que la caractéristique de sommet $deg_i$ peut être obtenue en sommant les éléments sur la ligne i ou la colonne i de la matrice d’adjacence (A).
La même année, Kier, Hall, Randic et ses collaborateurs [27-29] ont étendu $^1\chi$ pour des chemins plus longs que les bords de longueur L, et ont défini l’indice d’ordre L selon ($^L\chi$):
| $$\bbox[white,8px]{^L\chi = 1/2 \left(\sum_{i,j,k} deg_i \times deg_j \times … deg_L \right)^{-0.5} }\label{Kier}$$ |
où le produit des degrés de vertex est calculé avec des sommets situés le long de la distance topologique L. Pour prendre en compte la nature des atomes symbolisés par les sommets, Kier et Hall proposent l’utilisation d’indices de connectivité de vertex ($^L\chi^\nu$) [30] de la même manière que $^Lχ$ mais en utilisant des poids de valence delta ($δ^\nu_i$) au lieu de $deg_i$.
| $$\bbox[white,8px]{^L\chi^\nu = 1/2 \left(\sum_{i,j,k} δ^\nu_i \times δ^\nu_j \times … δ_L^\nu \right)^{-0.5} }\label{Kier1}$$ |
| $$\bbox[white,8px]{δ^\nu_i = (Z^\nu_i – H_i)/(Z_i-Z^\nu_i -1)}\label{Kier2}$$ |
Ici,
- $Z^\nu_i$ indique le nombre d’électrons de valence dans l’atome $\nu_i$
- $Z_i$ est son numéro atomique,
- $H_i$ est le nombre d’atomes d’hydrogène attachés à l’atome $\nu_i$.
Par exemple, dans le cas des amines aliphatiques,
- $δ^\nu_i$ = 3 pour l’azote dans le groupe amino primaire,
- dans le groupe amino secondaire $δ^\nu_i$ = 4,
- dans le groupe amino tertiaire δv i$δ^\nu_i$ = 5,
- les poids correspondants pour les atomes de carbone sont 1, 2, 3 ou 4, en fonction de l’environnement de liaison de l’atome.
Le tableau suivant indique les valeurs de $δ^\nu_i$ généralement admises pour différents atomes:
| Li | Na | K | Rb | Cs | Be | Mg | Ca | Sr | Ba | Cl | Br | I | S |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1/9 | 1/17 | 1/35 | 1/53 | 2 | 2/9 | 2/17 | 2/35 | 2/53 | 7/9 | 7/27 | 7/45 | 5/9 |
En 1991, Randic a introduit l’indice de connectivité vertex variable ($^Lχ^f$) [31] comme approche alternative à l’indice de Kier et Hall pour la caractérisation des hétérosystèmes dans les études QSPR-QSAR. La principale différence entre les deux descripteurs moléculaires est que l’ancien index utilise des poids de vertex optimisés ($deg^f_i$) et le dernier utilise des poids de vertex fixes ($deg_i$):
| $$\bbox[white,8px]{^Lχ^f = \left(\sum_{i,j,k} deg_i^f \times deg_j^f \times …. \times deg_L^f \right)^{-0.5} }\label{Randic}$$ |
Ce descripteur flexible peut être obtenu à partir d’une matrice d’adjacence modifiée ($A^{modif}$), où ses principaux éléments diagonaux ont été remplacés par des paramètres variables qui doivent être optimisés pour chaque type d’atome présent dans la molécule. Par exemple, la figure 1 montre le graphique sans hydrogène (Hydrogen-Suppressed Graph) [32, 33] de l’acide aminé hétérocyclique tryptophane:
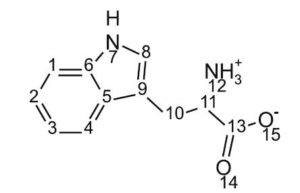
Le tableau 2 donne $A^{modif}$ avec le $deg_i^f$ correspondant à chaque sommet. Il convient de noter que pour des raisons de clarté, des atomes d’hydrogène peuvent être inclus pour les hétéroatomes dans le HSG. Dans les liaisons C – O, on a supposé un ordre de 1,5, avec une valeur de 1 pour les liaisons simples et de 2 pour les liaisons doubles. Clairement, dans le cas présent, $^Lχ^f $ dépend des variables optimisables x, y et z assignées aux atomes de carbone, d’oxygène et d’azote, respectivement.
L’indice peut être calculé en ajoutant les contributions des liaisons pour toutes les liaisons:
| $$ \bbox[white,8px]{\begin{matrix} ^1χ^f = 3/(3 + x) + 2/(4 + x) + 1/[(3 + x)(2 + x)]^{0.5}\\ + 1/[(2 + x)(4 + x)]^{0.5} + 4/[(3 + x)(4 + x)]^{0.5}\\ + 2/[(4 + x)(1.5 + y)]^{0.5} + 2/[(3 + x)(1 + z)]^{0.5} \\ + 1/[(4 + x)(2 + z)]^{0.5} \\ =f(x,y,z) \end{matrix}} $$ |
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Bibliographie
1. Wiener H (1947) J Am Chem Soc 69:17
2. Wiener H (1947) J Am Chem Soc 69:2636
3. Wiener H (1948) J Phys Chem 52:425
4. Wiener H (1948) J Phys Chem 52:1082
5. Stull DR, Westrum EF Jr, Sinke GC (1969) The chemical thermodynamics of organic compounds. Wiley, New York
6. Charkin OP (1972) Russ Chem Bull (Historical Archive) 21:1386
7. Van Krevelen DW (1990) Properties of polymers: their correlation with chemical structure; their numerical estimation and prediction from additive group contributions. Elsevier, Amsterdam
8. Bicerano J (2002) Prediction of polymer properties, revisited and expanded, 3rd edn. Marcel Dekker, New York
9. Nikiforov VA, Karavan VS, Miltsov SA, Selivanov SL, Kolehmainen E, Wegelius E, Nissinen M (2003) ARKIVOC 6:191 http://www.arkat-usa.org/ark/journal/2003/I06_Varvoglis/AV-744A/744A.pdf
10. Exner O, Bohm S (2001) Collect Czech Chem Commun 66:1623
11. Krenkel G, Castro EA, Toropov AA (2001) J Mol Struct Theochem 542:107
12. Duchowicz P, Castro EA, Toropov AA (2002) Comput Chem 26:327
13. Verguts T, Ameel E, Storms G (2004) Mem Cognit 32:379
14. Iwai Y, Yamanaga Sh, Arai Y (1999) Fluid Phase Equilib 163:1
15. Mazzobre MF, Roman MV, Morelle AF, Corti HR (2005) Carbohydr Res 340:1207
16. Ghafourian T, Barzegar-Jalali M (2002) Farmaco 57:565
17. Olsen E, Nielsen F (2001) Molecules 6:370 http://www.mdpi.org
18. Ren B (2002) Comput Chem 26:357
19. Thomsen M, Asmussen AG, Carlsen L (1999) Chemosphere 38:2613
20. Joback KG (2001) Fluid Phase Equilib 185:45
21. Casalenglo M, Sello G (2005) J Mol Struct Theochem 727:71
22. Balaban AT (1992) J Chem Inf Comput Sci 32:23
23. Randic M, Basak SC (1999) J Chem Inf Comput Sci 39:261
24. Barysz M, Jashari G, Lall RS, Srivastava VK, Trinajstic N (1983) In: King RB (ed) Chemical applications of topology and graph theory. Elsevier, Amsterdam
25. Ivanciuc O (2000) Rev Roum Chim 45:289
26. Randic M (1975) J Am Chem Soc 97:6609
27. Kier LB, Hall LH, Murray WJ, Randic MJ (1975) Pharm Sci 64:1971
28. Kier LB, Hall LH (1976) Molecular connectivity in chemistry and drug research. Academic, New York
29. Kier LB, Hall LH (1986) Molecular connectivity in structure-activity studies. Research Studies Press, Letchworth
30. Kier LB, Hall LH (1976) J Pharm Sci 65:1806
31. Randic M (1991) Chemometr Intell Lab Syst 10:213
32. Mekenian O, Bonchev D, Balaban AT (1984) Chem Phys Lett 109:85
33. Seybold PG, May M, Bagal UA (1987) J Chem Educ 64:575
34. Randic M, Dobrowolski JC (1998) Int J Quantum Chem 70:1209
35. Randic M, Mills D, Basak SC (2000) Int J Quantum Chem 80:1199
36. Randic M, Basak SC (2000) J Chem Inf Comput Sci 40:899
37. Randic M, Hansen PJ, Jurs PC (1988) J Chem Inf Comput Sci 28:60
38. Hansen PJ, Jurs PC (1988) J Chem Educ 65:574
39. Randic M (1991) J Mol Struct Theochem 233:45
40. Pogliani L (1992) J Pharm Sci 81:334
41. Pogliani L (1993) Comput Chem 17:283
42. Pogliani L (1993) J Phys Chem 97:6731
43. Pogliani L (1994) J Chem Inf Comput Sci 34:801
44. Pogliani L (1994) J Phys Chem 98:1494
45. Pogliani L (1997) Croat Chem Acta 70:803
46. Pogliani L (1997) Amino Acids 13:237
47. Pogliani L (1999) J Mol Struct Theochem 466:1
48. Pogliani L (2000) The concept of graph mass in molecular graph theory. A case in data reduction analysis. Nova, New York
49. Pogliani L (1996) J Chem Inf Comput Sci 36:1082
50. Pogliani L (1996) J Phys Chem 100:18065
51. Pogliani L (1997) Med Chem Res 7:380
52. Pogliani L (1999) J Chem Inf Comput Sci 39:104
53. Needham DE, Wei I, Seybold PG (1988) J Am Chem Soc 110:4186
54. Pogliani L (1995) J Phys Chem 99:925
55. Randic M (1991) New J Chem 15:517
56. Randic M (1991) J Chem Inf Comput Sci 31:311
57. Randic M (1994) Int J Quantum Chem Quantum Biol Symp 21:215
58. Ladik J, Appel K (1966) Theor Chim Acta 4:132
59. Toropov AA, Toropova AP (1998) Russ J Coord Chem 24:81
60. Toropov AA, Toropova AP (2001) J Mol Struct Theochem 538:287
61. Toropov AA, Nesterov IV, Nabiev OM (2003) J Mol Struct Theochem 622:269
62. Toropov AA, Toropova AP (2002) J Mol Struct Theochem 581:11
63. Toropov AA, Toropova AP (2002) J Mol Struct Theochem 578:129
64. Ivanciuc O, Ivanciuc T, Cabrol-Bass D (2002) J Mol Struct Theochem 582:39
65. Ganzalez OG, Murray JS, Peralta-Inga Z, Politzer P (2001) Int J Quantum Chem 83:115
66. Toropov AA, Toropova AP, Nesterov IV, Nabiev OM (2003) J Mol Struct Theochem 640:175
67. Basak SC, Grunwald GD (1995) J Chem Inf Comput Sci 35:366
68. Weininger D (1988) J Chem Inf Comput Sci 28:31
69. Weininger D, Weininger A, Weininger JL (1989) J Chem Inf Comput Sci 29:97
70. Weininger D (1990) J Chem Inf Comput Sci 30:237
71. http://www.daylight.com
72. Vidal D, Thormann M, Pons MJ (2005) J Chem Inf Model 45:386
73. Toropov AA, Toropova AP, Mukhamedzhanova DV, Gutman I (2005) Indian J Chem A 44:1545
74. Toropov AA, Toropova AP, Ismailov TT, Voropaeva NL, Ruban IN, Rashidova SSh (1996) Russ J Phys Chem 70:1081
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Liens GITHUB
- Une liste triée de documents ML (principalement en apprentissage profond) portant sur la chimie, la biologie et la découverte de médicaments.
- Démocratisation de l’apprentissage profond pour la découverte de médicaments, la chimie quantique, la science des matériaux et la biologie
- Démystification des réseaux neuronaux profonds multi-tâches pour les relations structure-activité quantitatives (DeepNeuralNet_QSAR)
- Flame : Framework pour la prise en charge la modélisation prédictive dans le cadre du projet eTRANSAFE (apprentissage automatique pour les modèles de type QSAR)
- QSAR/QSPR using descriptor-free molecular embedding
- FeatureCreature est un outil logiciel open-source pour la visualisation structurelle des explications QSAR (Quantitative Structure Activity Relations).
- Conception moléculaire de Novo utilisant les réseaux neuronaux récurrents et l’apprentissage par renforcement
- BMI219-2017-DeepQSAR :Apprentissage multitâche avec perceptron multi-couche pour QSAR
- Chainer Chemistry : une bibliothèque pour l’apprentissage en profondeur en biologie et en chimie
- generic-qsar-py-utils : objectif de ce projet: fournir un ensemble de fonctions Python (ou classes avec des méthodes associées) pouvant être utilisées pour effectuer une variété de tâches utiles à la génération de fichiers d’entrée, à partir de jeux de données cheminformatics, qui peuvent être utilisés pour construire et valider QSAR modèles (générés à l’aide de méthodes Machine Learning implémentées dans d’autres logiciels
- Classification des molécules en utilisant des réseaux de neurones artificiels
