Introduction
Toutes les cellules vivantes ont une membrane séparant l’intérieur de l’extérieur. De part et d’autre de la membrane, siège une tension électrique appelée potentiel membranaire.
En termes mathématiques, le potentiel membranaire VM est défini par
| $$\bbox[white,8px] {V_M=V_{in}-V_{out}.} $$ |
où $V_{in}$ est le potentiel à l’intérieur de la cellule et $V_{out}$ est celui à l’extérieur.
Ces potentiels vont changer pendant une phase active. Au repos, un neurone a typiquement un potentiel de -70 mV.
Un courant d’entrée correspond à un ion chargé positivement, tel que $Na^+$ entrant dans la cellule. Cela augmente le potentiel de la membrane, la portant à une valeur proche de zéro. Dans ce cas, la cellule est dite dépolarisée.
Un courant de sortie correspond soit à la sortie d’un ion chargé positivement tel que $K^+$ ou par l’entrée d’un ion chargé négativement comme $Cl^-$. Dans ce cas, la cellule devient hyper-polarisée.
La différence de potentiel provient des différences dans les concentrations de divers ions à l’intérieur et à l’extérieur de la cellule. Le maintien de la différence de potentiel implique également le transport d’ions à travers la membrane cellulaire et la perméabilité sélective de la membrane à ces ions.
Les ions principaux trouvés de chaque côté de la membrane cellulaire sont $Na^+$, $K^+$ et $Cl^-$. La concentration d’ions $K^+$ à l’intérieur d’une cellule est environ 10 fois supérieure à celle du liquide extracellulaire, alors que les concentrations de $Na^+$ et $Cl^-$ sont beaucoup plus élevés à l’extérieur de la cellule qu’à l’intérieur.
La bicouche lipidique de la membrane cellulaire est un mauvais conducteur du courant ionique car elle n’est pas perméable aux ions. Cependant, la membrane contient des protéines de canal qui permettent aux ions de se déplacer à travers elle.
Il existe deux types de canaux ioniques dans la membrane: à ouverture déclenchée et ceux toujours ouverts. Les canaux déclenchés peuvent s’ouvrir et se fermer et la probabilité d’ouverture dépend souvent du potentiel de la membrane; ceux-ci sont appelés canaux dépendants du voltage.
Les canaux déclenchés sont typiquement sélectifs pour un seul ion. La perméabilité de la membrane à un ion particulier dépend du nombre de canaux ouverts sélectifs pour cet ion. La plupart des canaux à déclenchement sont fermés au repos; par conséquent, les canaux ioniques toujours ouverts sont principalement responsables de l’établissement du potentiel de repos. Un potentiel d’action est généré lorsque les canaux à déclenchement sont ouverts, permettant le flux d’ions à travers la membrane cellulaire.
En raison des différences de concentration, lorsque les canaux appropriés sont ouverts, les ions $Na^+$ et $Cl^-$ ont tendance à diffuser dans la cellule, tandis que les ions $K^+$ ont tendance à se diffuser vers l’extérieur. Notez que les ions ne diffusent pas simplement dans ou hors d’un canal ouvert jusqu’à ce que la concentration de cet ion de chaque côté de la cellule soit nulle. C’est à cause du champ électrique créé par la séparation des charges positives et négatives à travers la membrane cellulaire.
Supposons, par exemple, que la cellule soit perméable uniquement à $K^+$. Le gradient de concentration de $K^+$ éloigne les ions $K^+$ de la cellule. Cependant, l’efflux continu de $K^+$ accumule un excès de charge positive à l’extérieur de la cellule et laisse derrière lui un excès de charge négative à l’intérieur. La charge négative est constituée principalement d’anions organiques imperméables $A^-$. Cette accumulation de charge agit pour empêcher l’efflux supplémentaire de $K^+$, de sorte qu’un équilibre est finalement atteint. A cet équilibre, les forces motrices électriques et chimiques sont égales et opposées (figure 1.1). Le potentiel de la membrane à laquelle les ions $K^+$ sont en équilibre à travers la membrane est appelé le potentiel de Kern Nernst, d’équilibre ou d’inversion.
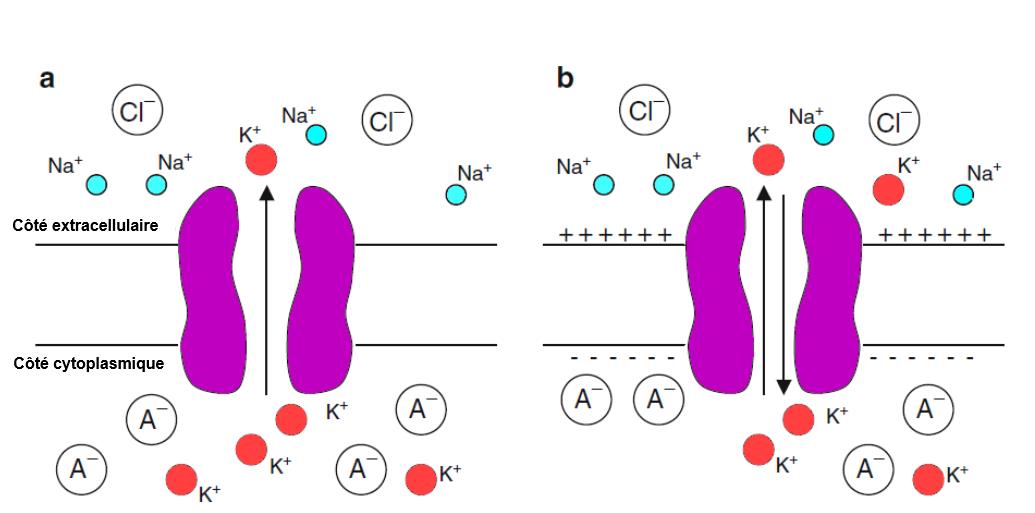
Fig 1.1 : le flux de $K^+$ est déterminé à la fois par le gradient de concentration de $K^+$ et par le potentiel à travers la membrane.
(a) Pour une cellule perméable uniquement à $K^+$, le gradient de concentration de $K^+$ éloigne les ions $K^+$ de la cellule.
(b) L’efflux continu de $K^+$ accumule un excès de charge positive à l’extérieur et un excès de charge négative à l’intérieur.
A l’équilibre, les forces motrices électriques et chimiques sont égales et opposées
Dans la section suivante, nous allons dériver l’expression suivante pour le potentiel de Nernst de $K^+$:
| $$\bbox[white,8px] {E_k=\frac{-RT}{zF} ln \frac{[K^+]_{in}}{[K^+]_{out}} } $$ |
Ici, $E_k$ est le potentiel de Kernernern, $R$ est la constante de gaz, $T$ est la température absolue en kelvin, $z$ est la valence de $K^+$, $F$ est la constante de Faraday et $[K^+]_{out}$ et $[K^+]_{in}$ sont les concentrations d’ions $K^+$ à l’extérieur et à l’intérieur de la cellule. Une formule similaire est valable pour les potentiels de Nernst pour $Na^+$ et $Cl^-$.
Les neurones au repos sont perméables à $Na^+$ et $Cl^-$ en plus de $K^+$. En raison de leurs différences de concentration, les ions $Na^+$ et $Cl^-$ se déplacent dans la cellule et les ions $K^+$ se déplacent vers l’extérieur.
L’afflux d’ions $Na^+$ tend à dépolariser la cellule, alors que l’efflux de $K^+$ et l’afflux de $Cl^-$ ont l’effet inverse.
Le potentiel de repos de la cellule est le potentiel auquel il existe un équilibre entre ces flux. Cela dépend des concentrations des ions à l’intérieur et à l’extérieur de la cellule, ainsi que de la perméabilité de la membrane cellulaire à chacun des ions. On note qu’au repos, beaucoup plus de $K^+$ et de $Cl^-$ canaux que les canaux $Na^+$ sont ouverts; par conséquent, le potentiel de repos de la cellule est déterminé principalement par le $K^+$ et $Cl^-$ Potentiels de Nernst. Dans les sections suivantes, nous allons dériver l’équation de Goldman-Hodgkin-Katz (GHK), qui exprime explicitement comment le potentiel de repos dépend des concentrations, à l’intérieur et à l’extérieur, d’ions et des perméabilités de la membrane aux ions .
Pour qu’une cellule maintienne un potentiel de repos constant, l’efflux d’ions $K^+$ doit équilibrer l’afflux d’ions NaC (ici, nous ignorons les ions $Cl^-$). C’est-à-dire que la séparation de charge à travers la membrane doit être constante. Si ces fuites d’ions stables continuaient sans opposition, alors les ions $K^+$ dans la cellule seraient épuisés, tandis que la concentration d’ions $Na^+$ à l’intérieur de la cellule augmenterait. Cela conduirait finalement à une perte des gradients ioniques, nécessaire pour maintenir le potentiel de repos.
La dissipation des gradients ioniques est empêchée par des pompes actives qui extrudent les ions $Na^+$ de la cellule tout en absorbant le $K^+$. La pompe $Na^+$-$K^+$ est une protéine membranaire intégrale qui échange trois ions $Na^+$ contre deux ions $K^+$. C’est probablement le transporteur d’ions le plus important dans les membranes biologiques; Cependant, il y a beaucoup d’autres protéines dans la membrane qui sont capables de pomper des ions d’un côté de la membrane à l’autre.
l’équation de Nernst
Nous allons dériver l’équation de Nernst puis celle de GHK.
Rappelons que si la membrane est perméable à un seul ion, alors le potentiel de cet ion sera le potentiel de repos pour lequel les forces électro-motrices et chimiques s’équilibrent. L’équation GHK est, dans un certain sens, une généralisation de l’équation de Nernst pour laquelle nous supposons que la membrane est perméable à plus d’un seul ion. L’équation GHK détermine le potentiel de repos tel que les forces électriques et chimiques générées par chacun de ces ions s’équilibrent.
La première étape dans la dérivation de ces équations est de dériver l’équation de Nernst-Planck.
soit $[C](x)$ la concentration d’un ion et $V(x)$ le potentiel à un point x à travers la membrane.
La loi de diffusion de Fick nous dit que le flux de diffusion est donné par
| $$\bbox[white,8px] {J_{diff}=-D\frac{\partial [C](x)} { \partial x }} $$ |
D est la constante de diffusion en $cm^2/sec$.
La concentration est en molécules par $cm^3$, de sorte que le flux diffusif a comme unté des molécules par $cm^2$. (Pensez au flux comme un mouvement à travers la surface de la cellule à deux dimensions.) La direction du mouvement va de fortes concentrations à de faibles concentrations.
La constante de diffusion (mesurée empiriquement) dépend de la taille de la molécule et du milieu dans lequel elle est diffusée. Une valeur typique pour les ions tels que $K^+$, $Cl^-$ et $Na^+$ est $2.5 \times 10^{-6}$ $cm^2/s$. L’ion calcium a une constante de diffusion d’environ un ordre de grandeur inférieur.
L’autre force physique responsable du mouvement passif des ions est la dérive électrique décrite par la version microscopique de la loi d’Ohm:
| $$\bbox[white,8px] {J_{drift}=-\mu z [C] \frac{\partial V} { \partial x }} $$ |
Le champ électrique, E équivalent à $\frac{\partial V} { \partial x }$, est le gradient du potentiel V (mesuré en volts) et a donc des unités de volts par centimètre. z est la valence de l’ion ($\pm 1$, $\pm 2$,etc.). Le paramètre $\mu$ est la mobilité et a des dimensions de $cm^2/sec/Volt$ et [C] est la concentration. Plus la concentration est élevée, plus la dérive est importante. Notez que la dérive a les mêmes dimensions que le flux diffusif.
Le flux total à travers la membrane est donné par la somme du flux diffusif et de la dérive électrique:
| $$\bbox[white,8px] {J_{total}= -D\frac{\partial [C](x)} { \partial x } -\mu z [C] \frac{\partial V} { \partial x }} $$ |
La relation d’Einstein relie la mobilité au coefficient de diffusion:
| $$\bbox[white,8px] {D= \frac{KT}{q} \times \mu } $$ |
où k est la constante de Boltzmann (J/K), T est la température absolue, et q est la charge (mesurée en coulombs). Ainsi, nous pouvons écrire le flux total comme :
| $$\bbox[white,8px] {J_{total}= -\frac{-\mu KT}{q} \times \frac{\partial [C]} { \partial x } -\mu \times z \times [C] \frac{\partial V} { \partial x }} $$ |
Il est commode de convertir cette équation, qui est en termes de nombre de molécules individuelles, en son équivalent molaire, en divisant par le nombre d’Avogadro. Il est également pratique d’introduire $RT=F$, où R est la constante de gaz idéale et F est la constante de Faraday, au lieu de $kT=q$. (Une liste de ces constantes est donnée à la fin de la section suivante.) Cela donnera un flux par mole. La multiplication de ce flux par la valence et la constante de Faraday produisent un flux de courant
| $$\bbox[white,8px] {I = -\left( u\times z\times RT \times \frac{\partial [C]} { \partial x } + u\times z^2\times F \times [C] \frac{\partial V} { \partial x } \right)} $$ |
$I$ est mesurée en ampères par $cm^2$. La quantité u est la mobilité molaire,$\frac{\mu}{N_A}$. Cette équation est appelée équation de Nernst-Planck.
L’équation de Nernst est obtenue en réglant le courant $I$ égal à zéro. En effet, pour une espèce ionique donnée, à l’équilibre, les effets de la diffusion et ceux électriques se compensent:
| $$\bbox[white,8px] {I = -\left( u\times z\times RT \times \frac{\partial [C]} { \partial x } + u\times z^2\times F \times [C] \frac{\partial V} { \partial x } \right) = 0} $$ |
| $$\bbox[white,8px] {\left(RT \times \frac{\partial [C]} { \partial x } + z\times F \times [C] \frac{\partial V} { \partial x } \right) = 0} $$ |
| $$\bbox[white,8px] {\left(\frac {RT}{zF} \times \frac{\partial [C]} {[C] } + \partial V \right) = 0} $$ |
soit
| $$\bbox[white,8px] {V_{eq} = V_{in} – V_{out} = -\frac {RT}{zF} \times ln \frac{[C]_{in}} {[C]_{out}} } $$ |
C’est-à-dire que le potentiel d’équilibre (ou Nernst), qui se produit lorsque tous les flux s’équilibrent, dépend du logarithme du rapport des concentrations des ions à l’intérieur et à l’extérieur de la cellule.
Appliquons l’équation de Nernst pour calculer le potentiel d’équilibre de $K^+$.
Dans une cellule de mammifère typique, il y a
- 140 mM de $K^+$ à l’intérieur de la cellule
- 5 mM de $K^+$ à l’extérieur de la cellule.
A température ambiante, 37°C, $RT/F = 26.73$ mV.
Par conséquent, le potentiel d’équilibre du potassium est $162 \times log \frac{140}{5} = -89.7$ mV.
L’équation de Nernst-Planck décrit le mouvement des ions chargés dans les milieux aqueux. Cependant, la membrane cellulaire a une épaisseur et il peut y avoir des barrières d’énergie ou des sites de blocage dans le canal. Dans ce cas, les ions circulant à travers le canal ouvert peuvent ne pas obéir à l’équation de Nernst-Planck et nous devons modéliser le comportement complexe dans la membrane pour obtenir une image réelle du flux à travers la cellule.
Ce type de biophysique est au-delà des détails qui sont nécessaires pour cette partie, mais l’équation qui en résulte joue un rôle dans les parties ultérieures.
Ainsi, nous présenterons une dérivation raccourcie d’une simplification de ce qui se passe dans la membrane.
Equation de Goldman, Hodgkin et Katz
Goldman, Hodgkin et Katz sont arrivés avec ce modèle simplifié appelé équation à champ constant. Ils ont supposé que
- le champ électrique à travers la membrane lipidique est constant,
- l’équation de Nernst-Planck tient dans la membrane,
- les ions se déplacent tous indépendamment.
Soit $V_M$ le potentiel total à travers une membrane de largeur l et soit V(x) le potentiel au point x à travers la membrane. Puisque le champ électrique est constant, $E=-V_M/l$. Ceci implique que $dV/dx=V_M/l$.
La mobilité des ions dans la membrane sera différente de celle de la solution aqueuse;
dénotons cette mobilité par $u^*$.
Enfin, soit $\beta$ le rapport de la solubilité ionique dans la membrane à la solubilité ionique dans la solution aqueuse.
Ainsi, si [C] est la concentration aqueuse, alors $\beta [C]$ est la concentration de la membrane. Avec ces hypothèses, l’équation de Nernst-Planck pour le courant à travers la membrane peut s’écrire :
| $$\bbox[white,8px] {I = -\left( u^* z^2 F\beta [C] \frac{V_M} {l} – u^* z RT \beta [C] \frac{d[C]} {dx} \right) \text{ avec } 0 < x < l} $$ |
L’équation ci-dessus est une équation différentielle ordinaire linéaire de premier ordre par rapport à $[C]$ soumis aux deux conditions aux limites
$[C](0)=[C]_{in}$ et $[C](l)=[C]_{out}$.
On ne peut pas, en général, résoudre une équation de premier ordre avec deux conditions aux limites.
Cependant, le courant I est inconnu, donc le choisir correctement nous permettra de trouver une solution qui satisfasse les deux conditions aux limites. Nous laissons cet exercice élémentaire au lecteur. Le résultat est
| $$\bbox[white,8px] {I = \frac {u^* z^2 F V_M \beta}{l}\left( \frac{[C]_{out} e^{- \xi} -[C]_{in}}{e^{- \xi} -1} \right) } $$ |
où $\xi = \frac{zV_M F}{RT}$
Cette expression est souvent écrite en termes de perméabilité, $P=\frac{\beta u^* RT}{lF}$, ce qui donne
| $$\bbox[white,8px] {I = PzF\xi \left(\frac{[C]_{out} e^{- \xi} -[C]_{in}}{e^{- \xi} -1} \right) } \label{ref1} $$ |
La perméabilité a comme dimension des centimètres par seconde. Ainsi, la dimension de I s’exprime comme un courant par unité de surface. L’équation ($\ref{ref1}$) est appelée équation à champ constant.
C’est le courant dû à une seule espèce ionique. Le courant s’annule à l’équilibre ou au potentiel de Nernst des espèces ioniques. Un tracé courant-tension (I -V) est commun.
Si les concentrations intérieure et extérieure sont identiques, le tracé I -V est linéaire. Pour $[C]_{out} > [C]_{in}$ (respectivement, $[C]_{out} < [C]_{in}$), le tracé I -V est concave vers le bas (concave vers le haut).
Le lecteur est encouragé à tracer le courant en fonction de la tension pour différents rapports de concentration.
Si les concentrations sont très différentes à l’intérieur et à l’extérieur, la courbe I-V est fortement rectifiante.
Cela signifie que l’amplitude du courant dépend fortement du fait que le potentiel soit supérieur ou inférieur à l’équilibre.
Étant donné plusieurs espèces ioniques, le courant total n’est qu’une somme des courants individuels.
C’est une conséquence de l’hypothèse 3, qui dit que les ions n’interagissent pas.
Supposons qu’il y ait trois ions perméables, $K^+$, $Na^+$ et $Cl^-$ avec des courants correspondants, $I_K$; $I_{Na}$ , et $I_{Cl}$: A l’équilibre, le courant total, $I= I_K + I_{Na} + I_{Cl}$, disparaît; c’est-à-dire, $I=0$: Le potentiel auquel cela se produit est
| $$\bbox[white,8px] {V_M = \frac{RT}{F} ln \frac{P_K[K]^+_{out} + P_{Na}[Na]^+_{out} + + P_{Cl}[Cl]^+_{in}}{P_K[K]^+_{in} + P_{Na}[Na]^+_{in} + + P_{Cl}[Cl]^+_{out}} } \label{ref2} $$ |
où les $P_j$ sont les perméabilités de chacune des trois espèces ioniques. C’est une généralisation de l’équilibre de Nernst discutée ci-dessus et s’appelle l’équation de Goldman -Hodgkin-Katz (GHK).
Avec une espèce, l’équation se réduit au potentiel de Nernst.
Par exemple, dans l’axone du calamar, les rapports des perméabilités, au repos, sont $P_K:P_{Na}:P_{Cl}=1:0.03:0.1$.
Les concentrations ioniques à l’intérieur de la cellule sont respectivement de $K^+$, $Na^+$ et $Cl^-$ de $400, 50$ et $40$ mM, alors qu’à l’extérieur de la cellule elles sont de $10, 460$ et $540$ mM. Ainsi, à température ambiante, l’équilibre ou potentiel de repos est d’environ $-74$mV.
$E_i= \frac {RT}{zF} ln \frac {[C]_{out}}{[C]_{in}}$ |
|||
|---|---|---|---|
| $T=20°C$ | |||
| $K^+$ | $124$ | $2.25$ | $58 \times log\frac {2.25}{124} = -101$ |
| $Na^+$ | $10.4$ | $109$ | $58 \times log\frac {109}{10.4} = +55$ |
| $Cl^-$ | $1.5$ | $77.5$ | $- 58 \times log\frac {77.5}{1.5} = -99$ |
| $Ca^{2+}$ | $10^{-4}$ | $2.1$ | $29\times log\frac {2.1}{10^{-4}} = 125$ |
| $T=20°C$ | |||
| $K^+$ | $400$ | $20$ | $58 \times log\frac {20}{400} = -75$ |
| $Na^+$ | $50$ | $440$ | $58 \times log\frac {440}{50} = +55$ |
| $Cl^-$ | $40$ à $150$ | $560$ | $- 58 \times log\frac {560}{40 \text{ à } 150} = -66 $ à $ – 33$ |
| $Ca^{2+}$ | $10^{-4}$ | $10$ | $29\times log\frac {10}{10^{-4}} = 145$ |
| $T=20°C$ | |||
| $K^+$ | $140$ | $5$ | $62 \times log\frac {5}{140} = -89.7$ |
| $Na^+$ | $5$ à $15$ | $145$ | $58 \times log\frac {145}{ 5\text{ à }15 } = 90 $ à $ 61$ |
| $Cl^-$ | $4$ | $110$ | $- 62 \times log\frac {110}{4} = -89$ |
| $Ca^{2+}$ | $10^{-4}$ | $2.5$ à $5$ | $31\times log\frac {2.5 \text{ à } 5}{10^{-4}} = 136$ à $145$ |
Constantes élémentaires
| $N_A$ | $6.022 \times 10^{23}$ mol (Nombre d’Avogadro) |
| k$ | $1.380658 \times 10^{-23}$ J/K (constante de Boltzmann) |
| $R$ | $8.31451$ J/(mol K) (constante des gaz parfaits) |
| $e$ | $1.602177\times 10^{-19}$ C (charge d’un électron ) |
| $F$ | $96485.3$ C/mol (constante de Faraday) |
| $\epsilon _0$ | $ 8.85 \times 10^{-12}$ F/m (constante de permittivité ) |
| $K$ | $Kelvin$ (°C = Kelvin + 273.16) |
| $L$ | $Litre$ |
| $N$ | $Newton$ |
| $J$ | $Joule (Nm)$; 1 J = 0.238845 cal |
| $V$ | $Volt(J/C)$ |
| $C$ | $Coulomb$ |
| $A$ | $Ampère(C/s)$ |
| $\Omega$ | $Ohm (V/A)$ |
| $S$ | $Siemens (A/V)$ |
| $F$ | $Farad (sA/V \text{ ou } C/V)$ |
Circuits équivalents: l’analogue électrique
Nous avons vu dans la section précédente que les propriétés électriques des cellules sont déterminées par les espèces ioniques qui les traversent. Les courants circulent en fonction des perméabilités des canaux ioniques et des gradients de concentration à travers la membrane cellulaire. Cependant, toute notre discussion jusqu’à présent a été dans un environnement stable. L’équation GHK ne détermine pas comment le potentiel membranaire change en réponse aux changements dans les perméabilités. Pour cette raison, on ne peut pas comprendre comment ces changements dans les perméabilités peuvent générer un potentiel d’action.
Une manière très utile de décrire le comportement du potentiel membranaire est en termes de circuits électriques; ceci est communément appelé le modèle de circuit équivalent . Le circuit se compose de trois composants:
- des conducteurs ou des résistances, représentant les canaux ioniques;
- batteries, représentant les gradients de concentration des ions;
- des condensateurs, représentant la capacité de la membrane à stocker la charge.
Le modèle de circuit équivalent conduit à une compréhension à la fois intuitive et quantitative de la façon dont le mouvement des ions génère des signaux électriques dans la cellule nerveuse.
Nous considérons d’abord une membrane qui est seulement perméable au potassium. Le circuit équivalent est représenté sur la Fig. 1.2. La bicouche lipidique qui constitue la membrane cellulaire a des propriétés diélectriques et, en tant que telle, se comporte de la même manière qu’un condensateur.
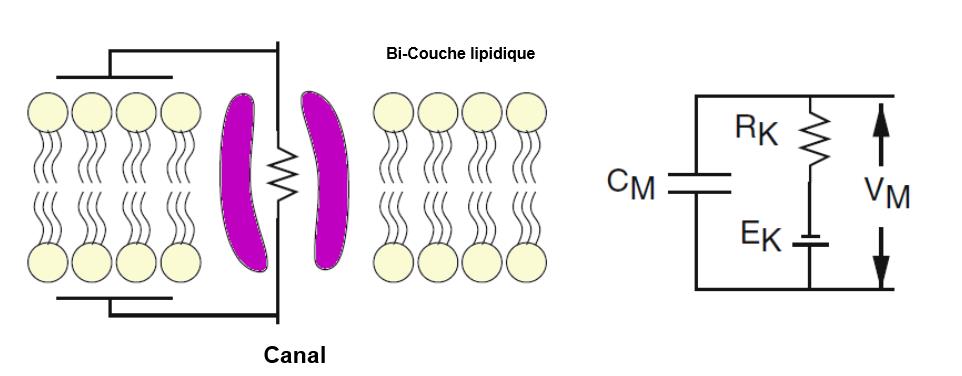Fig 1.2 : membrane montrant la couche isolante lipidique| $$\bbox[white,8px] {q=C_M \times V_M } \label{ref3} $$ |
Ainsi la charge totale q est proportionnelle au potentiel $V_M$ avec une constante de proportionnalité $C_M$ appelée capacitance membranaire.
Notez que la capacité totale dépend de la surface totale du diélectrique; ainsi, les plus gros neurones ont une capacité totale plus grande que les plus petits.
La capacitance par centimètre carré est appelée capacitance membranaire spécifique et sera notée $c_M$. Par conséquent, la capacité totale de la membrane $C_M$ est la capacité membranaire spécifique $c_M$ multipliée par la surface totale de la cellule.
En général, la capacitance membranaire spécifique peut dépendre du potentiel; Cependant, pour la plupart des membranes cellulaires, la capacité spécifique de la membrane est très proche de $1 \mu$F/$cm^2$.
Puisque le courant est la dérivée temporelle de la charge, nous pouvons différencier ($\ref{ref3}$), diviser par la surface de la cellule, et obtenir une expression pour le courant capacitif spécifique:
| $$\bbox[white,8px] {i_{cap}=c_M \frac{dV_M}{dt} } \label{ref4} $$ |
Nous avons ici le courant capacitif par unité de surface. Nous désignerons le courant capacitif total par $I_{cap}$.
Dans le circuit équivalent, les canaux $K^+$ sont représentés comme un conducteur en série avec une batterie. Si $\hat {g}_K$ est la conductance d’un seul canal $K^+$, alors, en utilisant la loi d’Ohm, le courant ionique à travers ce canal est
| $$\bbox[white,8px] {\hat{I}_{cap}=\hat {g}_K (V_M – E_k) } \label{ref5} $$ |
Ici, $E_k$ est le potentiel généré par la batterie qui est donné par le potentiel de Nernst de $K^+$. La force électro-motrice est $V_M$. Supposons maintenant qu’il existe $K_C$ = $N_K$ $K^+$ canaux dans une zone unitaire de membrane. Ceux-ci peuvent tous être combinés dans le seul circuit équivalent représenté sur la Fig. 1.2. La conductance par unité de surface ou conductance membranaire spécifique ($S/cm^2$) est donnée par $g_K = N_k \times \hat {g}_K$ et la résistance membranaire spécifique ($\Omega$ $cm^2$) est donnée par $r_K= \frac{1}{g_K}$. Comme le potentiel de Nernst dépend uniquement du gradient de concentration de $K^+$, et non du nombre de canaux $K_C$, il s’ensuit que le courant $K_C$, par unité de surface, est donné par
| $$\bbox[white,8px] {I_K=g_K (V_M – E_k) = \frac{V_M-E_K}{r_K} } \label{ref6} $$ |
La loi de Kirchhoff stipule que le courant total dans la cellule doit être égal à zéro. Avec la représentation du circuit équivalent, cela conduit à une équation différentielle pour le potentiel de la membrane:
| $$\bbox[white,8px] {0 = i_{cap} + I_K=c_M \frac{V_M}{dt} + \frac{V_M-E_K}{r_K} } \label{ref7} $$ |
soit
| $$\bbox[white,8px] {c_M \frac{V_M}{dt} = – \frac{V_M-E_K}{r_K} = g_K \times (V_M-E_K) } \label{ref8} $$ |
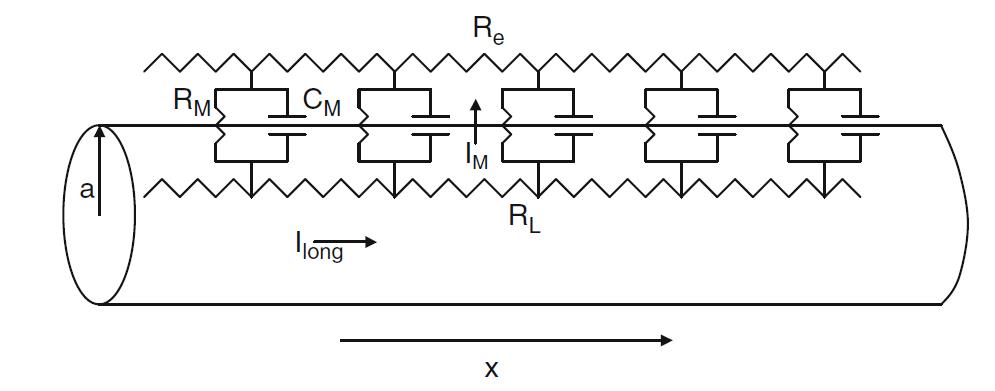
Fig 1.3 : Circuit équivalent pour une membrane avec 3 canaux.
| $$\bbox[white,8px] {i_{ion} = -g_{Cl}(V_M-E_{Cl}) – g_{Na}(V_M-E_{Na}) – g_K(V_M-E_K)} \label{ref9} $$ |
La source de courant n’est généralement pas exprimée en courant par unité de surface, donc nous devons diviser $I(t)$ par la surface totale A du neurone. Il s’ensuit que
| $$\bbox[white,8px] {c_M\frac{dV_M}{dt} = -g_{Cl}(V_M-E_{Cl}) – g_{Na}(V_M-E_{Na}) – g_K(V_M-E_K) + \frac{I(t)}{A}} \label{ref10} $$ |
Nous pouvons ré-écrire cette équation sous la forme :
| $$\bbox[white,8px] {c_M\frac{dV_M}{dt} = -\frac{(V_M-E_R)}{r_M} + \frac{I(t)}{A}} \label{ref11} $$ |
où $E_R= (g_{Cl}E_{Cl} + g_{Na}E_{Na} + g_KE_K) r_M$ est le potentiel au repos de la cellule et $r_M=\frac{1}{g_{Cl} + g_{Na} + g_K}$ est la resistance spécifique de la membrane.
Pour une membrane passive dans laquelle les conductances et les courants sont tous constants, $V_M$ atteindra un état stable:
| $$\bbox[white,8px] {V_{ss}=\frac{g_{Cl}E_{Cl} + g_{Na}E_{Na} + g_KE_K + I/A}{g_{Cl} + g_{Na} + g_K}} \label{ref12} $$ |
En l’absence du courant appliqué, le potentiel permanent est une somme pondérée des potentiels d’équilibre des trois courants. Ceci est similaire à l’équation GHK ($\ref{ref2}$), dans laquelle la contribution au potentiel de repos de chaque ion est pondérée proportionnellement à la perméabilité de la membrane à cet ion particulier.
Notez cependant que dans le modèle de circuit équivalent, l’équilibre est une somme linéaire pondérée des potentiels d’équilibre, alors que dans l’équation GHK, la somme est non linéaire.
Nous remarquons que la conductance membranaire et la perméabilité sont des concepts connexes; Cependant, ils ne sont pas les mêmes. La perméabilité dépend de l’état de la membrane, tandis que la conductance dépend à la fois de l’état de la membrane et de la concentration des ions.
La perméabilité à $K^+$, par exemple, peut être élevée s’il y a un grand nombre de canaux $K^+$ ouverts. Cependant, si la concentration en ions $K^+$ est faible des deux côtés de la membrane, la conductance de $K^+$ sera faible.
La constante de temps de la membrane
Dans cette section, nous allons voir comment une cellule passive isopotentielle répond à un courant appliqué. Cela aidera à expliquer comment chaque composant du circuit électrique contribue à des changements dans le potentiel de la membrane.
La cellule est dite passive si ses propriétés électriques ne changent pas pendant la signalisation. Une telle cellule ne peut pas générer de potentiel d’action; Cependant, il est important de comprendre comment les propriétés passives ou constantes d’une cellule influencent les changements dans le potentiel de la membrane avant d’envisager une signalisation active.
De plus, beaucoup de dendrites n’ont pas de canaux bloqués, donc leur comportement est principalement influencé par leurs propriétés passives.
La cellule est dite isopotentielle si le potentiel membranaire est uniforme à tous les points de la cellule; c’est-à-dire que le potentiel de la membrane dépend uniquement du temps. Pour simplifier l’analyse, nous allons considérer une cellule sphérique de rayon $\rho$.
Supposons que dans cette cellule, soit appliqué un courant ,$I(t)$, activé à $t=0$ à une valeur constante, $I_0$, et désactivé à $t=T$. Ici, nous supposons $I_0 > 0$; Cependant, cela n’est vraiment pas nécessaire.
Notez que pour une cellule isopotentielle, le courant injecté se répartit uniformément sur la surface. Il en résulte que pour une cellule sphérique, le courant circulant à travers une zone unitaire de la membrane est
| $$\bbox[white,8px] {I_{M}(t)=\frac{I(t)}{4 \pi \rho ^2}=\left\{\begin{array}{rl} \frac{I_0}{4 \pi \rho ^2} & \mbox{si 0 < t < T} \\ 0 & \mbox{sinon.} \end{array}\right.} \label{ref13} $$ |
Comme précédemment, supposons que $c_M$ soit la capacité membranaire spécifique, $r_M$, la résistance membranaire spécifique et $E_R$ le potentiel de repos de la cellule. Pour simplifier les choses, nous prenons $E_R=0$ de sorte que $V_M$ mesure l’écart du potentiel membranaire par rapport au repos.
Compte tenu de ($\ref{ref11}$), le potentiel membranaire satisfait l’équation différentielle ordinaire
| $$\bbox[white,8px] {c_M\frac{dV_M}{dt} = – \frac{(-V_M)}{r_M} + I_M(t)} \label{ref14} $$ |
Si la cellule commence au repos, alors la solution de cette équation linéaire satisfait
| $$\bbox[white,8px] {V_M(t)=\frac{r_M I_0}{4\pi \rho ^2} \left( 1_ e^{-\frac{t}{\tau _M }} \right) \text{ pour } 0 < t < T} \label{ref15} $$ |
où $\tau _M = c_M \times r_M$ est la constante de temps de la membrane.
| $$\bbox[white,8px] {V_M(t)=V_M(T) \times e^{-\frac{t}{\tau _M }} \text{ pour } t > T} \label{ref16} $$ |
La solution est illustrée sur les Figures 1.4a et 1.4b.
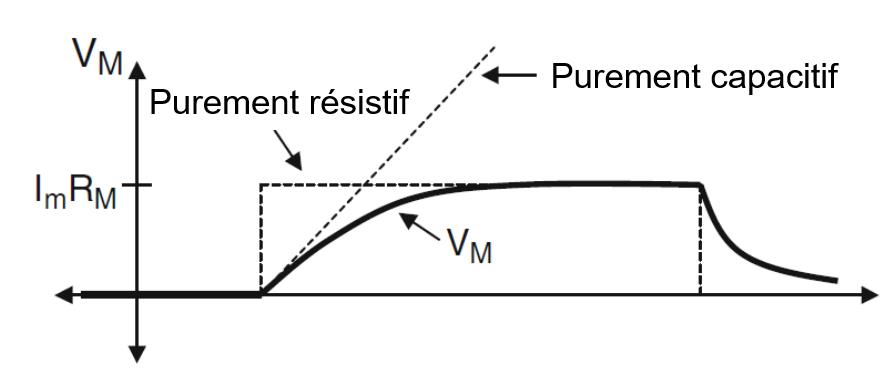
Fig 1.4a : Le changement du potentiel membranaire en réponse à une étape de courant.
Le potentiel de la membrane est représenté par une ligne continue.
Les lignes pointillées montrent les trajectoires temporelles des éléments purement capacitifs et résistifs.
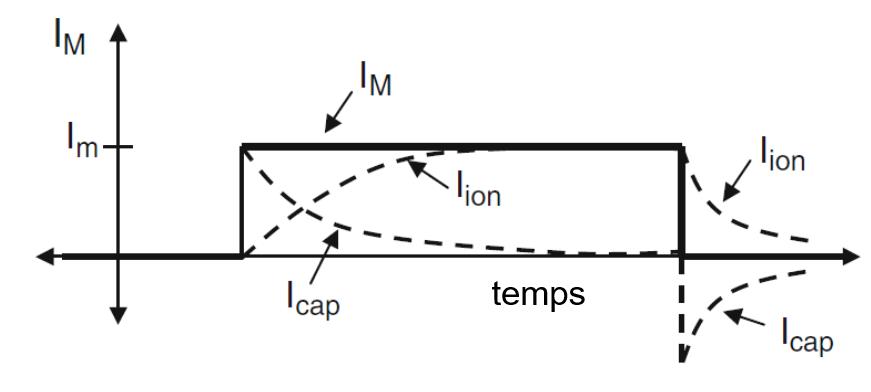
Fig 1.4b : cette figure montre l’évolution dans le temps du courant total de la membrane, du courant ionique et du courant capacitif
La constante de temps de la membrane détermine également la vitesse à laquelle le potentiel de la membrane décroît au repos après l’arrêt du courant. Le potentiel de la membrane à l’état stable satisfait
| $$\bbox[white,8px] {I_0 \frac{r_M }{4\pi \rho ^2} = I_0 R_{INP} } \label{ref17} $$ |
où $R_{INP}$ est la résistance d’entrée de la cellule.
Notez que si le courant d’entrée change de $\Delta I$, alors le potentiel de la membrane en régime permanent change par $R_{INP} \Delta I $; c’est-à-dire que la résistance d’entrée est la pente de la courbe $I-V$ obtenue en traçant la tension en régime permanent par rapport au courant appliqué.
L’augmentation initiale du potentiel membranaire est déterminée principalement par la capacité de la membrane. Initialement, la tension aux bornes de la résistance et celle aux bornes du condensateur sont toutes les deux nulles.
A partir de la loi d’Ohm, il s’ensuit qu’au début, aucun courant ne traverse la résistance et tout le courant est dû au condensateur.
En raison du courant capacitif, le potentiel à travers le condensateur, et donc le potentiel de membrane, deviendra plus positif. Au fur et à mesure que $V_M$ augmente, la différence de potentiel de la membrane commence à conduire le courant à travers la résistance de l’électrode, ce qui réduit le courant à travers le condensateur.
Finalement, le potentiel de membrane atteint une valeur où tout le courant de la membrane circule à travers la résistance. Cette valeur est donnée par $V_M=I_0 R_{INP}$.
Les figures 1.4a et 1.4b montrent également les réponses dans lesquelles il y a des éléments purement résistifs ou purement capacitifs. S’il n’y a pas de capacité de membrane, $V_M$ satisfait
| $$\bbox[white,8px] {V_M(t)=r_M \times I_M(t)} \label{ref18} $$ |
C’est-à-dire que $V_M$ passe au potentiel permanent, $I_0 R_{INP}$, dès que le courant injecté est activé et qu’il revient au repos dès que le courant est coupé. S’il n’y a qu’un élément capacitif, le potentiel de membrane change linéairement tant qu’il y a un courant appliqué.
L’équation de câble
Nous avons, jusqu’à présent, considéré les propriétés passives d’une cellule isopotentielle. Cette analyse peut être utilisée pour décrire le signal dans le corps de la cellule, qui peut se rapprochée de celui d’une sphère.
Cependant, il n’est clairement pas approprié pour étudier les propriétés électriques de l’axone ou des dendrites. Ceux-ci sont mieux approximés par des cylindres qui ne sont pas isopotentiels. Un signal de tension en dessous du seuil qui est initié en un point le long de l’axone ou de la dendrite diminuera en amplitude avec la distance du point d’initiation.
Il est important de comprendre comment la géométrie de la cellule affecte la propagation du signal. Le signal peut, par exemple, correspondre à l’entrée synaptique d’un autre neurone. Comprendre comment la géométrie affecte la propagation du signal va aider à déterminer si l’entrée synaptique provoquera un potentiel d’action pour la cellule.
Ici, nous supposons que la membrane est passive, de sorte que l’analyse soit plus applicable aux dendrites qu’aux axones. Cependant, comme nous le décrirons plus loin, la propagation passive du courant permet de déterminer la vitesse de propagation des potentiels d’action dans l’axone.
Nous considérons une cellule qui a la forme d’un long cylindre ou câble de rayon a. Nous supposons que le flux de courant est le long d’une seule dimension spatiale, x, la distance le long du câble. En particulier, le potentiel membranaire dépend uniquement de la variable x et non des composantes radiales ou angulaires.
L’équation du câble est une équation différentielle partielle qui décrit comment le potentiel membranaire $V_M(x,t)$ dépend des courants entrant, sortant et circulant dans le neurone. Le circuit équivalent est représenté sur la Fig. 1.5. Dans ce qui suit, nous supposerons $R_e=0$, de sorte que l’espace extracellulaire soit isopotentiel. Cette hypothèse est justifiée si le câble est dans un bain avec une grande surface transversale.
Nous considérons d’abord le courant axial circulant le long du neurone dû aux gradients de tension. Notez que la résistance totale du cytoplasme augmente proportionnellement à la longueur du câble et est inversement proportionnelle à la section transversale du câble. La résistivité intracellulaire spécifique, que nous désignons par $r_L$, est la constante de proportionnalité.
Par conséquent, un câble de rayon a et de longueur $\Delta x$ a une résistance totale de $R_L=r_L \Delta x/ \pi a^2$. Il résulte de la loi d’Ohm qu’à tout moment x, la diminution de $V_M$ avec la distance est égale à l’intensité du courant multiplié par la résistance.
| $$\bbox[white,8px] {V_M(x + \Delta x, t) – V_M(x , t)= -I_{long}(x,t)R_L = -I_{long}(x,t)\frac{\Delta x}{\pi a^2} r_L} \label{ref19} $$ |
Fig 1.5 : Circuit équivalent pour un câble passif uniforme. $I_{long}$ est le courant le long de l’intérieur du câble, $I_M$ est le courant à travers la membrane, $R_L$ est la résistance du cytoplasme, $R_e$ est la résistance de l’espace extracellulaire, $R_M$ est la résistance membranaire, $C_M$ est la capacité membranaire.
| $$\bbox[white,8px] {\text{si } x \rightarrow 0 \text{, } I_{long}(x,t)= \frac{\pi a^2}{r_L} \frac{\partial V_M(x,t)}{\partial x}} \label{ref20} $$ |
Soit $i_{ion}$ le courant par unité de surface dû aux ions entrant et sortant de la cellule. Alors, le courant ionique total qui circule à travers une membrane de rayon a et de longueur x est donné par $I_{ion} = (2\pi a \Delta x) i_{ion}$.
Rappelons que la vitesse de variation du potentiel de la membrane est déterminée par la capacité. La capacitance totale d’une membrane est égale à la capacité membranaire spécifique $c_M$ multipliée par la surface totale de la membrane.
Donc, pour un câble de rayon a et de longueur x, la capacité totale est donnée par $C_M= (2\pi a \Delta x) c_M $ et la quantité de courant nécessaire pour changer le potentiel de membrane à un taux $\partial V_M/\partial t$ est
| $$\bbox[white,8px] {I_{cap}(x,t)= (2\pi a \Delta x) c_M \frac{\partial V_M}{\partial t}} \label{ref21} $$ |
D’après la loi de Kirchhoff, la variation du courant axial intracellulaire est égale à la quantité de courant qui circule à travers la membrane. Par conséquent,
| $$\bbox[white,8px] {I_{cap}(x,t) + I_{ion}(x,t)= -I_{long}(x + \Delta x,t) + I_{long}(x,t) } \label{ref22} $$ |
Il s’ensuit :
| $$\bbox[white,8px] {(2\pi a \Delta x)c_M \frac{\partial V_M}{\partial t} + (2\pi a \Delta x)i_{ion} = \frac{\pi a^2}{r_L} \frac{\partial V_M(x + \Delta x, t)}{\partial x} – \frac{\pi a^2}{r_L} \frac{\partial V_M(x,t)}{\partial x} } \label{ref23} $$ |
Nous divisons les deux côtés de cette équation par $2 \pi a \Delta x$ et appliquons $x \rightarrow 0 $ afin d’obtenir l’équation du câble:
| $$\bbox[white,8px] {c_M \frac{\partial V_M}{\partial t} = \frac{a}{2r_L} \frac{\partial ^2 V_M}{\partial x^2} – i_{ion}} \label{ref24} $$ |
Pour un câble passif, dans lequel le potentiel de repos est supposé nul, $i_{ion}=V_M(x,t)/r_M$ où $r_M$ est la résistance membranaire spécifique. Ainsi l’équation ($\ref{ref24}$) devient
| $$\bbox[white,8px] {c_M \frac{\partial V_M}{\partial t} = \frac{a}{2r_L} \frac{\partial ^2 V_M}{\partial x^2} – \frac{V_M}{r_M}} \label{ref25} $$ |
Nous pouvons ré-écrire cette équation sous la forme
| $$\bbox[white,8px] { \tau _M \frac{\partial V_M}{\partial t} = \lambda ^2 \frac{\partial ^2 V_M}{\partial x^2} -V_M \\ } \label{ref26} $$ où $ \lambda = \sqrt{ \frac{a r_M}{2r_L}}$ et $\tau _M=c_M \times r_M $ sont respectivement la constante de longueur ou d’espace et la constante de temps de la membrane. |
Notez que la constante d’espace dépend de la géométrie du câble, c’est-à-dire du diamètre du câble; Cependant, ce n’est pas le cas de la constante de temps.
Nous présenterons plus loin une analyse détaillée des solutions à l’équation du câble et des propriétés des dendrites passifs. Pour le moment, il est instructif d’envisager des solutions stables.
Supposons, par exemple, que nous ayons un câble semi-infini (défini pour $x > 0$) et que nous injections un pas de courant, $I_0$, à $x=0$. Comme $x \rightarrow \infty $, la solution $V_M(x,t)$ approche une solution stable $V_{ss}(x)$ qui ne dépend pas du temps. En définissant $\frac{\partial V_M}{\partial x}$ dans ($\ref{ref26}$), nous trouvons que $V_{ss}$ satisfait
| $$\bbox[white,8px] {\lambda ^2 \frac{\partial ^2 V_{ss}}{\partial x^2} – V_{ss} = 0} \label{ref27} $$ |
Pour résoudre cette équation, nous avons besoin de conditions aux limites. Compte tenu de l’équation ($\ref{ref20}$), à savoir $I_0(x,t)= – \frac{\pi a^2}{r_L} \frac{\partial V_M}{\partial x}$, il s’ensuit que $V_{ss}$ doit satisfaire la condition suivante:
| $$\bbox[white,8px] {\frac{dV_{ss}}{dx}(0)= – \frac{r_L}{\pi a^2} I_0} \label{ref28} $$ |
La solution des équations ($\ref{ref27}$) et ($\ref{ref28}$) est
| $$\bbox[white,8px] {= – \frac{\lambda r_L}{\pi a^2} I_0 e^{\frac{-x}{\lambda}}} \label{ref29} $$ |
Notez que le potentiel de la membrane décroît exponentiellement. La distance à laquelle le potentiel décroit de $1/e$ est la constante d’espace.
Comme la constante d’espace est proportionnelle à la racine carrée du rayon du câble, nous concluons que les axones ou dendrites plus épais ont des constantes d’espace plus grandes que ceux plus étroits. Autrement dit, des axones ou dendrites plus épais transmettent des signaux sur de plus grandes distances.
Comme nous le verrons plus tard, ceci est important car cela influence la capacité du neurone à sommer spatialement les potentiels synaptiques entrants.
De plus, la conductance électrotonique, ou passive, joue un rôle important dans la propagation du potentiel d’action.
Les cellules plus épaisses avec une plus grande constante d’espace sont plus facilement excitées et sont capables de générer des potentiels d’action plus rapides.
La résistance d’entrée est définie comme étant le potentiel de la membrane en régime permanent, évalué à $x=0$, divisé par le courant injecté, ce qui donne :
| $$\bbox[white,8px] {R_{inp}(x)= V_{ss}(0)/I_0 =\frac{\lambda r_L}{\pi a^2} = \frac{1}{\pi a^{3/2}} \sqrt{\frac{r_M r_L}{2}}} \label{ref30} $$ |
Le potentiel d’action chez le calamar
Nous avons jusqu’à présent vu la membrane en tant que câble passif. Cependant, les câbles linéaires ne peuvent transmettre des informations sur de longues distances que si le câble a un diamètre énorme. Par exemple, l’axone du calamar mesure plus de 5 cm de long, a un diamètre d’environ 0,5 mm, une résistance à la membrane au repos de 700 $\Omega \text{ } cm^2 $, et une résistance transmembranaire de $r_L= 30 \Omega \text{ } cm$.
Ainsi, la constante d’espace pour l’axone du calmar est $\lambda =5.4 mm$. C’est un ordre de grandeur plus petit que la longueur.
Si le potentiel à une extrémité de l’axone est maintenu à 120 mV au-dessus du repos, alors le potentiel à l’autre extrémité est d’environ 10 $\mu V$ au-dessus du reste, soit un décrément de 10 000 fois. Pour que les signaux neuronaux puissent atteindre n’importe quelle distance, il doit y avoir une autre façon de les transporter afin qu’ils ne se dégradent pas.
La nature a résolu ce problème en insérant des canaux voltage-dépendants dans les membranes de nombreux types de cellules. Ces canaux sont des protéines qui laissent sélectivement différentes espèces ioniques dans la cellule. De plus, la perméabilité des canaux dépend de l’environnement local à proximité du canal. En particulier, pour les canaux voltage-dépendants, le fait que le canal soit ouvert ou fermé dépend du potentiel local proche du canal. C’est l’ouverture et la fermeture des canaux voltage-dépendants qui est responsable de la génération du potentiel d’action qui se propage le long de l’axone.
Hodgkin et Huxley (1952) ont été les premiers à fournir une description quantitative complète des courants régénératifs générant le potentiel d’action. Le choix de l’axone du calamar était fortuit puisque les propriétés électriques dépendent principalement des ions $Na^+$ et $K^+$. Considérons le circuit équivalent montré sur la Fig. 1.6 et supposons que la cellule soit isopotentielle. Alors, le potentiel de la membrane satisfait à
| $$\bbox[white,8px] {c_M \frac{dV}{dt} = -g_{Na}(V-E_{Na})-g_{K}(V-E_{K})-g_{L}(V-E_{L})} \label{ref31} $$ |
Dans l’équation ci-dessus, nous écrivons $V$ au lieu de $V_M$ et $I_L \equiv g_{L}(V-E_{L})$ s’appelle le courant de fuite.
Il correspond à un flux passif d’ions à travers des canaux non allongés. La conductance de fuite, gL, est constante. Puisque la plupart des canaux non allongés sont perméables aux ions $K^+$, $E_{L}$ est proche de $E_{K}$. Les conductances $g_{Na}$ et $g_{K}$ peuvent changer avec le temps car elles correspondent à l’ouverture et à la fermeture des canaux $Na^+$ et $K^+$, respectivement. Au repos, $g_{K}$ est environ 30 fois plus grand que $g_{Na}$, de sorte que l’état de repos est proche de $E_{K}$ à environ 65mV.
Supposons que nous puissions augmenter la conductance de $g_{Na}$ de 100 fois plus, alors le potentiel de repos serait beaucoup plus proche du potentiel de Nernst de l’ion $Na^+$, qui est d’environ 55mV.
Ainsi, l’amplification du potentiel, comme lors d’un potentiel d’action, implique des changements dans les conductances relatives des espèces ioniques dominantes. L’idée de Hodgkin et Huxley fut que les canaux voltage-dépendants fournissent le substrat pour cette régulation dynamique des conductances.
Les mécanismes de base sous-jacents aux potentiels d’action sont les suivants (figure 1.7).
Au repos ①, la plupart des canaux de $Na^+$ sont fermés, de sorte que le potentiel membranaire est principalement déterminé par le potentiel de Nernst de $K^+$. Si la cellule est dépolarisée au-delà d’un certain seuil, les canaux $Na^+$ s’ouvrent ➁ et cela dépolarise davantage la cellule.
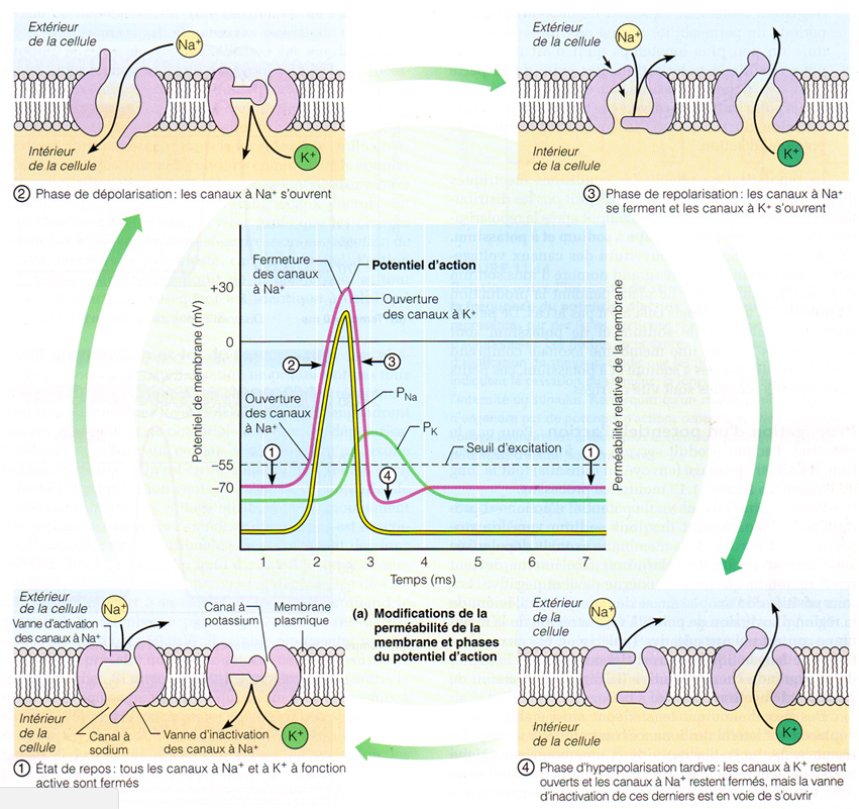Fig 1.7
Cela permet à plus de canaux de $Na^+$ de s’ouvrir, permettant à plus d’ions $Na^+$ d’entrer dans la cellule et forçant la cellule vers le potentiel Nernst de $Na^+$. C’est la course ascendante du potentiel d’action. Le canal $Na^+$ est transitoire, donc même quand ils sont dépolarisés, les canaux de $Na^+$ ont fini par s’arrêter.
Pendant ce temps, la dépolarisation ouvre les canaux $K^+$ ➂ et les ions $K^+$ sortent de la cellule. Cela hyperpolarise la cellule lorsque le potentiel membranaire se déplace vers le potentiel d’équilibre de $K^+$. Jusqu’à ce que les canaux $K^+$ voltage-dépendants se referment, la membrane est réfractaire. Pendant ce temps, les pompes échangent des ions $Na^+$ en excès à l’intérieur de la cellule avec des ions $K^+$ en excès à l’extérieur de la cellule.
Seul un très petit changement dans la concentration des ions $Na^+$ est nécessaire pour générer un potentiel d’action ➃.
D’après les mesures, nous constatons qu’environ 53 millions d’ions $Na^+$ doivent diffuser à travers la membrane pour la dépolariser de -60 à 50 mV. Cet afflux d’ions $Na^+$ représente seulement une variation de 0,012% de la concentration interne de $Na^+$, qui est typiquement d’environ 12 mM. Par conséquent, des changements dans la séparation des charges locales, et non dans la concentration, sont nécessaires pour un potentiel d’action.