Définissons une coque mince comme un corps délimité par deux surfaces courbes rapprochées. Supposons que chaque point de la coque soit associé aux coordonnées curvilignes $\alpha_1, \alpha_2$ et au vecteur normal unitaire $\overline{m}$, de telle sorte que la distance le long de $\overline{m}$ soit donnée par $z (- 0,5h (\alpha_1, \alpha_2) \leqslant z \leqslant 0,5h (\alpha_1, \alpha_2))$ .
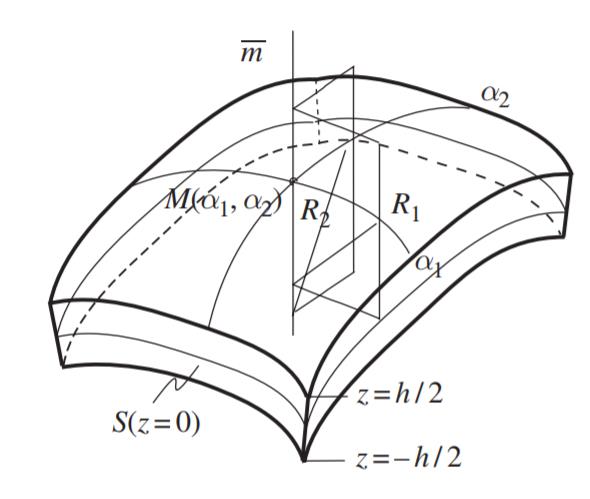
Ce corps est appelé coquille d’épaisseur h. Nous supposons que les faces de cette coquille sont lisses sans singularités. La coquille est classée comme mince ou épaisse sur la base du rapport $\frac{h}{R_i}$, où $R_i$ sont les rayons de courbure de la surface médiane S de la coquille, c’est-à-dire la surface à z = 0. Ainsi, la coquille est considérée comme mince si $max(\frac{h}{R_i})) \leqslant \frac{1}{20}$. Dans les autres cas, elle est considérée comme épaisse.
Cependant, il convient de noter que l’estimation ci-dessus est très approximative et, dans de nombreuses applications pratiques, d’autres caractéristiques géométriques et mécaniques devraient également être prises en compte.
La plupart des organes du corps humain, y compris le globe oculaire, l’œsophage, l’estomac, la vésicule biliaire, l’utérus, l’uretère et la vessie, peuvent être considérés comme des coquilles minces. Leur haute endurance et leur grande fonctionnalité dépendent des propriétés biomécaniques des tissus dont elles sont constituées et des arrangements spécifiques des constituants (protéines, fibrilles, cellules) en leur sein. Les tissus biologiques sont considérés comme des composites anisotropes, hétérogènes, incompressibles. Ils sont intrinsèquement non linéaires dans leur réponse mécanique et subissent des déformations finies.
De plus, la plupart des tissus biologiques, à l’exception des os, sont mous. Leurs caractéristiques sont les suivantes :
- ils sont fins,
- ils possèdent une faible raideur en réponse à l’allongement,
- ils ne résistent pas à la compression et à la flexion,
- ils subissent de grandes déformations,
- ils génèrent des contraintes latérales (cisaillement)
- ils peuvent se plisser en cours de fonctionnement sans perte de stabilité de l’organe.
Les propriétés ci-dessus définissent le degré élevé de variabilité des formes que l’organe peut prendre en charge.
L’aspect anatomique distinctif des organes est également corrélé avec leurs avantages structuraux. Ils contiennent l’espace optimal à l’intérieur et à l’extérieur, présentent des degrés élevés de résistance réservée et d’intégrité structurelle combinés à une fonctionnalité biomécanique efficace, présentent des rapports force / poids optimaux et sont idéaux pour résister à la pression interne et aux charges externes. Par exemple, l’estomac humain est l’organe du tractus gastro-intestinal situé dans le quadrant supérieur gauche de l’abdomen. Son rôle principal est d’accueillir et de digérer la nourriture. Même avec une petite épaisseur de la paroi gastrique, qui varie de 3 à 5 mm chez les sujets normaux, et le rayon de courbure $R_i$ caractéristique de la surface moyenne variant de 10 cm à 15 cm, il est capable de contenir de 2 à 5 litres de contenu gastrique mixte sans augmenter la pression intraluminale.
L’utérus d’une femme enceinte est l’organe en forme poire qui occupe l’abdomen inférieur et moyen. Ses principales fonctions sont d’accueillir et de nourrir le fœtus pendant la gestation, et d’expulser le bébé pendant le travail et l’accouchement. L’épaisseur de la paroi utérine dans différentes régions varie entre 0,5 et 1,5 cm et les rayons de courbure varient entre 20 et 40 cm. Par conséquent, l’utérus d’une femme enceinte peut également être approchée comme une coquille molle mince.
Ces dernières années, il est devenu possible de développer des modèles complexes des organes abdominaux et de mieux comprendre les mécanismes physiologiques cachés de leur fonction (Miftahof et al., 2009; Pullan et al., 2004; Cheng et al., 2007, Corrias et Buist, 2007, Pal et al., 2004, Pal et al., 2007). Un premier modèle biomécanique de l’organe en tant que coquille biologique molle a été développé par Miftakhov (1983c). Sous des hypothèses générales d’orthotropie curviligne et de non-linéarité physique et géométrique, une formulation mathématique et une étude numérique de la dynamique de la répartition contrainte-déformation dans l’organe sous des charges simples et complexes ont été réalisées. La dynamique du développement d’états uniaxiaux soumis à des contraintes dans le cardia et le pylore en fonction de la pression intraluminale a été démontrée par calcul et confirmée expérimentalement.
Les résultats ont fourni un aperçu précieux sur le mécanisme du traumatisme abdominal contondant avec rupture de la paroi antérieure de l’estomac et ont donné une explication biomécanique pour le syndrome de Mallory-Weiss. On pensait auparavant que des changements atrophiques dans la muqueuse gastrique et la couche sous-muqueuse étaient responsables de larmes longitudinales dans la région cardia-fundique et de saignements intragastriques potentiellement mortels. Les études du modèle à coque souple ont démontré que la structure anatomique et la configuration de l’estomac en soi rendent ces régions plus sensibles que les autres aux ruptures linéaires.
La biomécanique de l’intestin grêle a été largement étudiée expérimentalement et numériquement. Miftahof fut le premier à construire un modèle biophysiquement plausible de l’organe sous la forme d’une coquille biologique cylindrique molle. Grâce à ce modèle, il était possible de reproduire une variété de phénomènes d’ondes électromécaniques, y compris le réflexe progressif, les mouvements pendulaires, la segmentation et le péristaltisme. Le modèle contenait également des mécanismes neurorégulateurs intrinsèques – les plexus nerveux entériques et les neurotransmetteurs multiples. Ainsi, le modèle a permis d’étudier les effets de différentes classes de composés pharmacologiques sur la motilité de l’intestin grêle dans des conditions normales et pathologiques.
Des modèles mathématiques d’organes viscéraux traitant de divers aspects physiologiques ont été récemment proposées. Cependant, tous les modèles, sans exception, reposent sur une approche «mécaniste» réductionniste et ont donc une plausibilité biologique et des implications limitées pour notre compréhension de la physiopathologie de diverses maladies. Ceci est souvent dû à des applications indiscrètes et erronées d’idées et de méthodes empruntées à la mécanique des solides pour décrire leur comportement mécanique. Il faut souligner que la biomécanique n’est pas seulement la transformation des lois générales et des principes de la mécanique pour l’étude des phénomènes biologiques, mais plutôt le développement et l’extension adéquats de ces lois et des principes à la modélisation et à l’analyse des êtres vivants.
Par conséquent, des modèles intégratifs précis incorporant diverses données et servant de base à l’analyse multiniveaux des processus biologiques interdépendants sont nécessaires.
De tels modèles auront un impact énorme sur le démêlage des mécanismes complexes cachés des maladies et contribueront à la conception de leur traitement.
Malheureusement, il est encore courant dans la communauté des « modélisateurs » d’utiliser le système des équations de Navier-Stokes lors de la modélisation des viscères abdominaux creux en tant que structure ‘coque’. En utilisant des logiciels disponibles dans le commerce et des outils graphiques très flexibles, ils parviennent à ajuster les résultats des simulations numériques aux données expérimentales. L’approche est totalement incorrecte et les résultats causent de la confusion, plutôt que de fournir des solutions à des problèmes cliniques urgents.
Ainsi, il est erroné de prétendre que l’activité des ondes de contraction antrale joue le rôle dominant dans les mouvements des fluides intragastriques, sur la base des résultats des simulations par ordinateur d’un écoulement provoqué par des indentations prescrites des limites de surface.
Ce dernier système est censé représenter un modèle bidimensionnel de l’estomac. Il n’est pas surprenant que la méthode numérique, qui prédétermine les modèles d’écoulement souhaités, produise des résultats semblables à ceux observés expérimentalement, dans des études utilisant l’imagerie par résonance magnétique. Un modèle mathématique adéquat du phénomène ci-dessus aurait dû comprendre le système combiné des équations du mouvement de la coquille – l’estomac – et des équations de Navier-Stokes pour le contenu gastrique.
De plus, compte tenu de la propriété mécanique fondamentale du tissu, sa douceur, il est imprudent de soutenir qu’il existe une dépendance des états contrainte-déformation sur les rayons de courbure des organes viscéraux (Liao et al., 2004). Il est de la responsabilité d’un mathématicien appliqué, d’un informaticien et d’un ingénieur en mécanique de suggérer un descripteur adéquat et de donner une formulation mathématique rigoureuse du modèle.
Bien que les modèles de l’estomac et du petit et gros intestin comme coquilles biologiques décrits ici aient une valeur biomédicale limitée, ils sont mathématiquement solides et sont basés sur l’extension et l’application précises des lois générales et des hypothèses de la mécanique des coquilles molles . Ils intègrent des données électrophysiologiques et morphologiques concernant la structure et la fonction des organes humains et reproduisent quantitativement et qualitativement la dynamique de l’activité des ondes électromécaniques et la répartition contrainte-déformation. Ils peuvent servir de point de départ pour d’autres expansions et améliorations biologiques.
