Géométrie intrinsèque
Considérons une surface lisse S dans un espace euclidien tridimensionnel. Le système de référence est du type cartésien orthogonal $x_1$, $x_2$, $ x_3$. S est également associé avec un ensemble de paramètres indépendants $\alpha_1$ et $\alpha_2$.
$$x_1=f(\alpha_1,\alpha_2) \text{ , } x_2=f(\alpha_1,\alpha_2) \text{ et } x_3=f(\alpha_1,\alpha_2) \label{ref1} $$
où $f_j \text{ ( j=1, 2, 3) } $ sont des fonctions à une seule variable, indéfiniment dérivables.
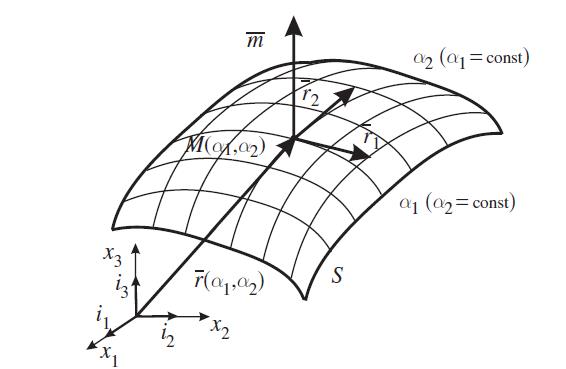
 En fixant α1 à une constante c et en faisant varier le paramètre $\alpha_2$ dans fj (c, $\alpha_2$), on obtient une courbe sur S. En donnant successivement à $\alpha_1$ une série de valeurs constantes on obtient une famille de courbes où seul le paramètre $\alpha_2$ varie . Ces courbes sont appelées les lignes de coordonnées $\alpha_2$. De même, en fixant $\alpha_2$ à une constante, on obtient les lignes de coordonnées $\alpha_1$- de S. Nous supposons qu’une seule courbe de la famille passe par un point de la surface donnée. Ainsi, tout point sur S peut être traité comme une intersection croisée des lignes de coordonnées curvilignes $\alpha_1$ et $\alpha_2$.
En fixant α1 à une constante c et en faisant varier le paramètre $\alpha_2$ dans fj (c, $\alpha_2$), on obtient une courbe sur S. En donnant successivement à $\alpha_1$ une série de valeurs constantes on obtient une famille de courbes où seul le paramètre $\alpha_2$ varie . Ces courbes sont appelées les lignes de coordonnées $\alpha_2$. De même, en fixant $\alpha_2$ à une constante, on obtient les lignes de coordonnées $\alpha_1$- de S. Nous supposons qu’une seule courbe de la famille passe par un point de la surface donnée. Ainsi, tout point sur S peut être traité comme une intersection croisée des lignes de coordonnées curvilignes $\alpha_1$ et $\alpha_2$.
La position d’un point M par rapport à l’origine O du système de référence est
défini par le vecteur de position $\overline{r}$,
$$\overline{r} = \overline{i}_1 x_1 + \overline{i}_2 x_2 + \overline{i}_3 x_3 = \sum_{i=1}^3 {\overline{i}_i x_i} $$
où {$\overline{i}_1 \text{, } \overline{i}_2 \text{, }\overline{i}_3$} est un repère orthonormé associé à {$x_1 \text{, } x_2 \text{, } x_3$}.
En vertu de l’équation ($\ref{ref1}$), $\overline{r}$ peut être ré-écrit :
$$\overline{r} = \overline{i}_1 f_1(\alpha_1,\alpha_2) + \overline{i}_2 f_2(\alpha_1,\alpha_2) + \overline{i}_3 f_3(\alpha_1,\alpha_2) \label{ref2} $$
Cette équation ($\ref{ref2}$) est appelée équation vectorielle de la surface S. En différenciant $\overline{r}$ par rapport à $\alpha_i \text{ ( i=1, 2, 3) } $, les vecteurs tangents aux lignes aux coordonnées $\alpha_1$, $\alpha_2$ sont définis par :
$$ \overline{r_1} =\frac{\partial{\overline{r}_1}}{\partial{\alpha_1}}\text{ , } \overline{r}_2 =\frac{\partial{\overline{r}_2}}{\partial{\alpha_2}}
$$
Les normes et les produits scalaires de $\overline{r}_1$ et $\overline{r}_2$ sont définis par
$$
\begin{array}{r c l}
\|\overline{r}_1\| = \overline{r}_1\text{ }\overline{r}_1 = A_1 = \sqrt{a_{11}} \\
\|\overline{r}_2\| = \overline{r}_2\text{ }\overline{r}_2 = A_2 = \sqrt{a_{22}}\\
\overline{r}_1\text{ }\overline{r}_2= A_1 A_2 \cos{\chi} = \sqrt{a_{12}}
\end{array}
\label{ref3}$$
où $\chi$ est l’angle entre les lignes de coordonnées, $A_i$ les paramètres de Lamé et $a_{ik}$ les coefficents du tenseur métrique A sur S.
En utilisant les équations ($\ref{ref3}$), nous introduisons les vecteurs unités $\overline{e_i}$ dans la direction de $\overline{r_i}$ qui sont décrits par
$$\overline{e_1}=\frac{\overline{r}_1}{\| \overline{r}_1 \|} = \frac{\overline{r}_1}{A_1} \text{ et } \overline{e}_2=\frac{\overline{r}_2}{\| \overline{r}_2 \|} = \frac{\overline{r}_2}{A_2} $$
Le vecteur $\overline{m}$, normal à $\overline{r}_1$ et $\overline{r}_2$ est trouvé à partir de
$$
\begin{array}{l c l}
\overline{m} = \overline{r}_1 \times \overline{r}_2 \\
\overline{m}\text{ }\overline{r}_1 = 0 \\
\overline{m}\text{ }\overline{r}_2 = 0
\end{array}
$$
où $\overline{r}_1 \times \overline{r}_2$ est le produit vectoriel donnant le vecteur $\overline{m}$ . Les vecteurs $\overline{r}_1$, $\overline{r}_2$ et $\overline{m}$ sont linéairement indépendants.
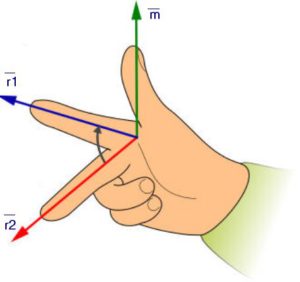
Ces vecteurs $\overline{r}_1$, $\overline{r}_2$ et $\overline{m}$ forment une base covariante {$\overline{r}_1$, $\overline{r}_2$ , $\overline{m}$} sur S.
La base réciproque {$\overline{r}^1$, $\overline{r}^2$ , $\overline{m}$} est définie par
$$
\begin{array}{l c l}
\overline{r}^1 = \frac{\overline{r}_1 \times \overline{m}}{\overline{r}_1 (\overline{r}_1 \times \overline{m})} \\ \overline{r}^2 = \frac{\overline{r}_2 \times \overline{m}}{\overline{r}_2 (\overline{r}_2 \times \overline{m})} \\
\end{array}
$$
